Electrostatic Potential and Capacitance Class 12 | Chapter 2 | Physics |
Table of Contents
Electrostatic Potential and Capacitance Class 12 | Chapter 2 | Physics | CBSE |
Electrostatic Potential and Capacitance
(I) Electrostatic Potential
Electrostatic potential energy is the amount of work done in bringing a charge from one point to the electric field against the electric field without change in kinetic energy.
Note that work done by an electric field in moving a given test charge from one point to another depends only on the initial and final points position . It does not depend on the path chosen in going from one point to another. Thus; electrostatic potential energy is conservative in nature.
W external = -q x 12∫E.dl = q x ΔV
Dimensional formula for electrostatic potential difference is
ΔV = WAB / q = [M L2 T-3 A-1]
SI unit of electrostatic potential difference is 1 volt. That is why potential difference is sometimes referred as voltage: 1 V = 1 J / 1 C = 1 NmC-1
Electrostatic potential difference between any two points in an electrostatic field is said to be 1 volt, when one joule of work is done in moving a positive charge of one coulomb from one point to another against the electrostatic force of field without any acceleration.
Electrostatic potential at any point in a region of electrostatic field is the minimum work done in carrying a unit positive charge from infinity to that point. VB = W∞B / q
Conservative Nature of Electrostatic Potential
A physical quantity which depends on initial and final positions only or does not depend on path followed by it is said to be conservative in nature.
Let a charge qo moves from A to B through path 1 and Q to P through path 2
WAB = qo (VB-VA) …..(i)
When test charge is taken from A to B
WBA = qo (VA-VB) ……(ii)
Adding equation (i) and (ii); we get
WAB + WBA = qo (VB-VA+ VA-VB)
WAB + WBA = 0
Thus, Electric potential is conservative in nature.
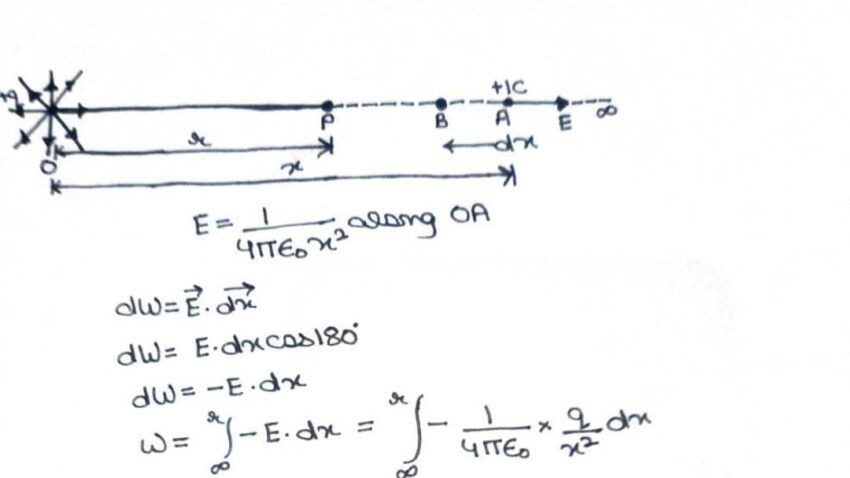
Electrostatic Potential due to a Point Charge
Suppose we have to calculate electric potential at any point P due to single point charge +q at O; where OP = r
By definition, electrostatic potential at P is that the amount of work done in carrying a unit positive charge from ∞ to P.
As work done does not depend on the path, we have to opt a expedient path along the radial direction from infinity to point P without acceleration.
At some intermediate A on this path where OA = x, the electrostatic force on the unit charge is

Equipotential Surfaces
An equipotential surface is that surface at every point of which same electric potential is present.
We know, potential difference between two points B and A = Work done in carrying unit positive test charge from A to B, i.e., VB – VA = WAB
If points A and B lie on equipotential surfaces, then VB = VA
∴ WAB = VB - VA = 0
Important Properties of Equipotential Surfaces
- Work is done in moving a test charge from one point to another point on an equipotential surface is zero
- Electric field is always tangential to the equipotential surface
- Two equipotential surfaces can never cross or overlap each other.
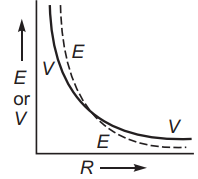
- Equipotential surfaces are closer in the regions of strong electric field and they are farther apart in the region of weak electric fields.
Pattern of Equipotential Surface
Equipotential Surfaces due to point charge
Equipotential Surface due to two an electric dipole
Equipotential Surface due to uniform electric field
Equipotential Surface due to an Two positive charges
Question : Why are electric Field lines perpendicular at some extent on an equipotential surface of conductor?
Answer: Electric field lines are perpendicular at a point on an equipotential surface because if they are not perpendicular then there will be a non zero component of electric field along the equipotential surface which causes the work to be done which is not possible.
Question : What is the amount of work done in moving a point charge around a circular arc of radius r at the centre of which another point charge is located.
Answer: The amount of work done in carrying a charge on an equipotential surface is always zero.
Principle of Superposition of Potentials
Let q1, q2 …….qn be n positive charges placed at r1, r2 …rn from point A
Potential at A due to q1 (V1) = kq1 / r1
Potential at A due to q2 (V2) = kq2 / r2
.
.
Potential at A due to qn (Vn) = kqn / rn
Total potential at A due to n charges (V) = V1 + V2 + V3 + …….. Vn
Related
Relation Between Electric Field and Electric Potential
Let; a charge + Q is placed at point O. A test charge qo is placed at point A
Let A and B be two points separated by distance dr. The two points A and B are so close that field between them remains almost constant.
The external force required to move the test charge qo (without acceleration) against the electric field E is given by
F = -qo E
Work done to move the test charge from A to B is
W = F . dr = – qo E. dr … (i)
Also work done in moving test charge from A to B is
W = Charge x potential difference = qo (VB – VA) = qo . dv ….(ii)
Equation equations (i) and (ii) ;
-qo E. dr = qo . dv
E = -dv / dr
The quantity dV /dr is the rate of variation of potential with distance and is called potential gradient. Thus the electric field at any point is adequate to the negative of potential gradient at that time. The negative sign indicates that the direction of electric field is in the direction of diminishing potential. Moreover the field is in the direction where this decline is steepest.
Question: A test charge Q is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure.
(i) Calculate the potential difference between A and C
(ii) At which point the electric potential is more and why?
Solution: (i) electric field intensity and potential energy are related as
E = -dV / dr
dV = -E .dr
Vc -VA = -4 E
(ii) As VC – VA = -4E is negative
VC < VA
Potential is greater at point A than point C, as potential decreases along the direction of electric field.
Question: Why do equipotential surface get close to each other near the point charge?
Answer: Equipotential surfaces get close to each other near the point charges as strong electric field is produced there.
E = -dV / dr
For a given equipotential surface small dr represent strong electric field and vice versa.
Question: Why the potential inside a hollow spherical charged conductor is constant and has the same value as on its surface?
Solution: Electric field inside the hollow spherical charged conductor is zero. So, no work is done in moving a charge inside the shell. Thus, potential is constant and therefore, equal to its value at the surface, i.e., V = 1 / 4π εo . q / r
Electric Potential Energy for two Charge Particles in Absence of External Electric Field
Suppose a point charge q1 is at rest at a point P1 in space. It takes no work to bring the first charge q1 since there is no field yet to work against.
∴ W1 = 0
Electric potential due to charge q1 at point P2 at distance r12 from P1 will be

W2 = potential x test charge

Electric Potential Energy for two Charge Particles in Absence of External Electric Field
Now we bring in the charge q3 from infinity to the point P3. Work has to be done against the forces exerted by q1 and q2.
Therefore; W3 = potential at P3 due to q1 and q2
Hence electrostatic potential energy of the system q1 + q2 + q3 is
U = Total work done to assemble the three charges = W1 + W2 + W3
Potential Energy for a Single Charge in an External Field
We have to determine the potential energy of a charge q in an external field E at a point P where the corresponding external potential is V.
We know; V at a point P is the amount of work done in bringing a unit positive charge from infinity to the point P.
Thus the work done in bringing a charge Q from infinity to the point P will be qV , i.e., W = qV
The work done is stored as a potential energy of the charge q. If r is the position vector of point P relative to some origin, then
Potential energy of a single charge q at r in external field = q. V r
Potential Energy for a System of Two Point Charges in an External Field
Let V r1 and V r2 the electric potentials of the field E at the points having vectors r1 and r2
Work done in bringing q1 from ∞ to r1 against the electric field = q1 V r1
Work done in bringing q2 from ∞ to r2 against the electric field = q2 V r2
Work done on q2 against the force exerted by q1 = 1 / 4πεo . q1 q2 / r12
where r12 is the distance between q1 and q2
Total potential energy of the system = The work done in assembling the two charges
U = q1 V r1 + q2 V r2 + 1 / 4πεo . q1 q2 / r12
Electric Potential due to Charged Ring
Let q be total charge distributed over a ring of radius R
dl be small element length
dq be charge on portion dl
Variation of Electric Potential (V) with distance (x) for a ring
Special Cases
1)If x >>> R ; R2 is neglected
V = Kq / x2 ; Ring behaves as point charge
2) At centre of ring
x = 0
V = kq / R
Electric Potential due to Uniformly Charged Spherical Shell
Potential at a point outside the shell ( r > R )
E = Kq / r2
E = -dV / dr
dV = -E.dr
dV = Kq / r2 .dr
Integrating both sides
∫dV = Kq ∫ 1 / r2 .dr
V = Kq / r
Potential at the surface of shell ( r = R)
V = Kq / R
Potential inside the shell
We know; inside the shell E = 0 and dV = -E . dr
dV = 0, i.e., V is constant inside the shell
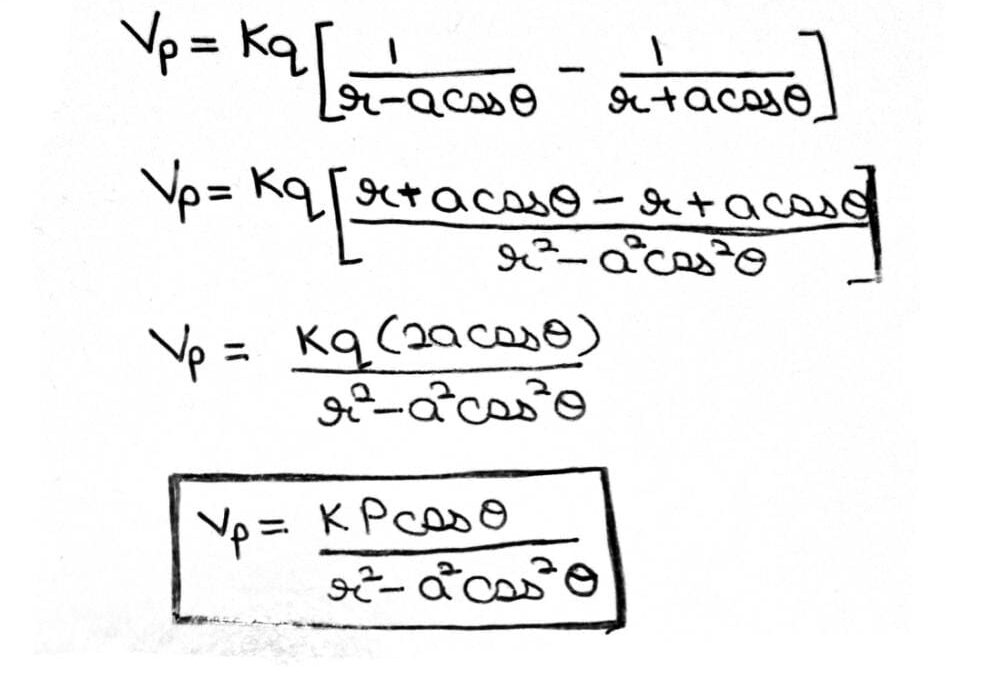
Electric Potential at any point due to an Electric Dipole
Let an electric dipole consisting of two equal and unlike point charges -q at A and +q at B, separated by a small distance AB = 2a, with centre at O. The dipole moment P = q x 2a
Let us take the origin at the centre of dipole. We have to calculate electric potential at any point P where OP = r. Let the distance of point P from charge -q at A be r1, i.e., AP = r1 and distance of point P from charge + q at B be r2, i.e., BP = r2
Electrostatic potential at P due to -q charge at A: VA = -kq / r1
Electrostatic potential at P due to -q charge at B: VB = kq / r2
VP = VA + VB = -kq / r1 + kq / r2
Construction : AN perpendicular CN , BM perpendicular CN
In Δ AON ; Cos θ = ON / OA = ON / a
a Cos θ = ON
Similarily; OM = a Cos θ
r1 = AP ≈ NP = CO + ON = r + a Cos θ
r2 = BP ≈ MP = CO – OM = r – a Cos θ
Special Cases
1)For short dipole; if r>>>a then a2 is neglected
2) On axial Line; θ = 0° [ cos 0° = 1 ]
V axial = KP / r2
3) On equatorial line; θ = 90° [ cos 90° = 1]
V equatorial = 0
Thus, potential at a point on equatorial line is zero
Question : A bird perches on a naked high power line and nothing happens to the bird. The same line is touched by a man standing on the ground and he gets deadly shocked?
Answer: The whole body of bird is at constant potential. Charge does not flow and no shock is produced. The man touching the ground maintains a potential difference among the different parts of his body. A large current flows which electrolysis blood and give rise to death.
Question : Three charges -q, +Q and -q are placed at constant distances on a straight line. If the potential energy of the three charge system is zero. Find the ratio Q / q
Answer: As the Net potential energy of this system is zero
1 / 4πεo [ -q Q / r + (-q) (-q) / 2r + Q (-q) / r ] = 0
-Q + q / 2 – Q = 0
2 Q = q / 2
Q / q = 1 / 4 = 1 : 4
Electrostatic Shielding
The phenomenon of creating a region free from electric field is called electrostatic shielding. It is based on the fact that electric field vanishes in the interior of the cavity of a hollow conductor.
Applications of Electrostatic Shielding
- In a thunderstorm accompanied by lightning, it is safest to sit inside a car, rather than near a tree or on the open ground since the metallic body of the car behaves as electrostatic shielding from lightning.
- Sensitive components of electronic devices are protected or shielded from outer electric annoyance by placing metal shields around them.
(II) Electrostatic Capacitance
Capacitor is a device that stores charge in the form of energy and capacitance is the ability of device to store charge in the form of energy.
When some charge is given to an insulated conductor, it gains a certain potential. On increasing the charge , an increase in potential also takes place. Thus , Q ∝ V or Q = CV
The probability constant C is called as electrical capacitance of the conductor.
The Capacitance of capacitor depends upon the following factors:
- Shape and size of the conductor
- Permittivity of the surrounding medium
- Presence of the other conductor in its neighbouring.
The SI unit of the capacitance is Farad. The capacitance of a capacitor is said to be 1 farad if the addition of a charge of 1 coulomb increases its potential by 1 volt.
Dimensional formula of capacitance = [M-1L-2T4A2]
Principle : Capacitor is based on the principle that capacitance of a capacitor can be incrased by bringing it near an earth connected uncharged conductor.
Capacitance of an Isolated Spherical Conductor
Let the radius of isolated spherical conductor be R.
Let the charge Q be uniformly distributed over its entire surface.
The potential at any point on the surface of spherical conductor will be given as
V = K Q / R
Capacitance of the spherical conductor situated in vacuum is
C = Q / V = Q / ( KQ / R)
C = 4 π εo x R
Thus, capacitance of a spherical isolated conductor is directly proportional to its radius.
Capacitance of Earth
Radius of earth = 6400 x 103 m
Capacitance of earth = (1 / 9 x 109) x 6400 x 103 = 711 μF
Parallel Plate Capacitor
It consists of two large plane and parallel conducting plates separated a small distance.
Capacitance of a Parallel Plate Capacitor
Let A be the area of each plate
d be the distance between two plates
±σ be uniform surface charge densities on two plates
±Q = ±σ A be total charge on each plate
Electric field intensity between the plates (E) = σ / εo = q / A εo
We know; E = V / d
∴ V = E d = (q / A εo) x d
Capacitance (C) = q / V = q / [(q / A εo) x d ]
Capacitance (C) = A εo / d
- Capacitance of a parallel plate capacitor is directly proportional to area of plates
- Capacitance of a parallel plate capacitor is inversely proportional to distance between plates
- Capacitance of a parallel plate capacitor also depends on nature of medium
- If a dielectric of permittivity ε occupies the space between the conducting plates ; then C = Aε / d
Relative Permittivity or Dielectric Constant
Dielectric Constant of a medium is the ratio of the electrostatic force of attraction among two given point charges separated by some distance apart in air to the force of attraction between the same two charges separated by same distance apart in the material medium.
K = Capacitance of a capacity with dielectric among the plates / Capacitance of the same capacitor with vacuum among the plates
Energy Stored in a Charged Capacitor
The process of charging up a capacitor by transferring of the electric charges from one plate to another. Certain amount of work done is required which is stored in the form of electrical potential energy.
Let; q be charge on plate of capacitor
dq be amount of charge transferred
Work done to store electric potential energy in capacitor (dw) = dU = V. dq = (q / C).dq
Total increase in potential energy = ∫ dU = U = 0Q∫ (q / C).dq
U = Q2 / 2 C
This is the required expression for energy stored in capacitor
Now We know; Q = CV
U = C2V2 / 2C = 1 / 2 CV2
U = 1 / 2 CV2
Also; C = Q / V
U = (1/2) (Q /V) (V2) = (1/2) QV
U = (1/2) QV
Electrostatic Energy Density in a Parallel plate Capacitor
An electric field is generated in the region between the plates of capacitor on charging it. Thus, work done in charging process is used in setting up the electric field. Presence of an electric field implies stored energy.
Energy stored per unit volume of space between the plates of capacitor is defined as energy density.
Energy density = Energy / Volume
This is the required expression for energy density in a parallel plate capacitor.
Grouping of Capacitor
Series Combination
Charge on each capacitor remains same and equals to the main supplied by the battery while potential distributes.
When negative plate of a capacitor is connected to positive plate of second capacitor and the negative of second capacitor is connected to positive plate of third one and so on, the capacitors are said to be connected in series.
This is required expression of equivalent capacitance in series combination
The reciprocal of equivalent capacitance is equal to sum of reciprocal of the individual capacitances .
The equivalent capacitance is comparably smaller than the individual capacitance.
Parallel Combination
When positive plate of all capacitors are connected to one common point and the negative plate of all capacitors are connected to another common point, them capacitors are said to be connected in parallel combination.
The potential difference across each capacitor is same while the charge on each capacitor is proportional to its capacitance.
Total charge stored in the capacitance is given as Q = Q1 + Q2 + Q3 = C1V + C2V + C3V
Let Cp be the equivalent capacitance of parallel combination ; Q = Cp . V
Cp . V = C1V + C2V + C3V
Cp = C1 + C2 + C3
Cp = C1 + C2 + ……..+ Cn
The equivalent capacitance is equal to the sum of individual capacitances
The equivalent capacitance is larger than the individual capacitance.
If n identical capacitors are connected in parallel ; Ceq = n C and Q’ = Q / n
Common Potential
When two capacitors of different capacitance and charged to different potentials are connected by a conducting wire then charge flows from higher potential to lower potential.
Until the potential becomes equal ; this flow of charge continues. The equal potentials attained by their capacitors is called common potential.
Note : In the process of sharing of charge, charge lost is zero.
Charge lost by one capacitor = Charge gained by another capacitor
Let C1 , C2 be capacitors of capacitances at V1 , V2 potentials respectively
Total Charge before sharing = C1V1 + C2V2
Let V be the common potential on sharing charges
Total charge after sharing = C1V + C2V
Total charge before sharing = Total charge after sharing
C1V1 + C2V2 = C1V + C2V
V = C1V1 + C2V2 / C1 + C2
When two capacitors are connected in parallel
V = C1V1 – C2V2 / C1 + C2
Loss of Energy on Sharing Charges
Let C1 and C2 be the capacitances
V1 and V2 be the potential of two conductors before they are connected
Potential energy before connection will be given as
After connection, let V be the common potential
V = C1V1 + C2V2 / C1 + C2
Potential energy after connection will be given as
Loss in the energy U = Ui – Uf
Capacitance of a Parallel Plate Capacitor with a Dielectric Slab
Let ; ± Q be the charges on the capacitor plates
A be area of each plate
d be thickness of dielectric slab
t be thickness of dielectric slab
E o be applied electric field
E p be induced electric field in dielectric slab
E = Eo – Ep be net electric field in the region of slab
The molecules in the slab get polarized in the direction of Eo on introducing a dielectric slab of thickness t < d
The electric polarisation vector P which is in the direction of Eo induces an electric field Ep opposite to the direction of Eo. Thus Net electric field inside the dielectric slab will be E = Eo – Ep
Outside the dielectric slab, field will be Eo only.
Potential difference between two plates of capacitor = Electric field x distance
On dividing numerator and denomenator by d , we get
Thus, C > Co ; Clearly on introducing a dielectric slab between plates of capacitor, its capacitance increases.
If t = d, i.e., dielectric slab fits completely inbetween plates of capacitor
Then C = KCo
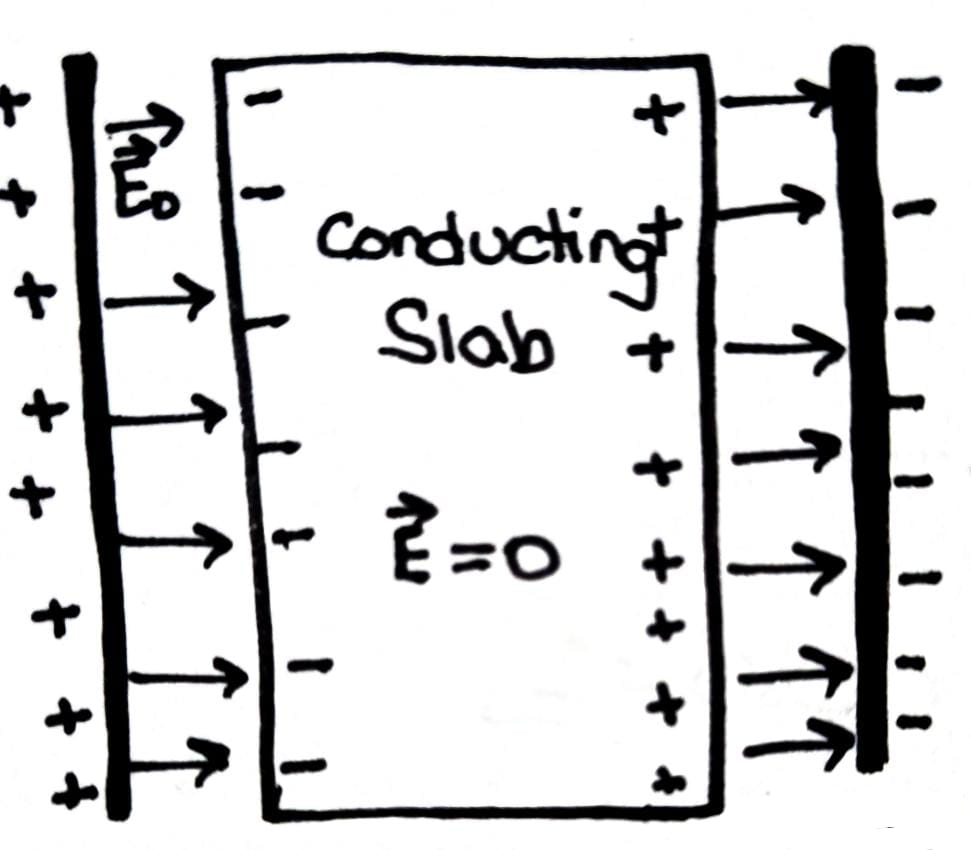
Capacitance of a Parallel Plate Capacitor with a Conducting Slab
Let t be thickness of conducting slab
A be the area of conducting slab
d be the distance between two oppositely charged plates
Eo be uniform electric field that exists over a distance (d – t)
Potential difference between the plates; V = Eo (d-t)

On dividing numerator and denomenator by d , we get
If t = d, i.e., thickness of conducting slab is equivalent to distance between the parallel plates then C = ∞
Dielectrics
Dielectrics are substance which permits charges to exert electrostatic force on one another but does not allow flow of charges through it. These are essentially insulators which on small localised displacement of its charges can be easily polarized.
Polar Molecule: When the centre of mass of positive charges or protons tends to coincide with centre of mass of negative charges or electrons, the molecule is said to be a polar molecule. Example: HCl , H2O , NH3
Non Polar Molecule : When centre of mass of positive charges coincide with centre of mass of negative charges the molecule is said to be non polar molecule. Example : N2 , O2, H2
Polarization
The process of formation of a polar molecule from a non polar molecule by applying external electric field is called polarization. P = εo Χ E
Here χ is constant of proportionality
Polarization of a non polar dielectric in an external electric field
- The dipole moment of a non polar molecule in absence of external electric field is zero.
- On applying external electric field, the centre of positive charges are displaced in the direction of external field while the centre of negative charges are displaced in the direction opposite to that of external field.
- This displacement of charges continue till the force exerted by external field is balanced by restoring force due to internal field.
- As a result a non-polar molecule is stretched to a polar molecule which is called as induced electric dipole.
- This non polar molecule remains as a polar molecule till an electric field is applied across it.
Polarization of a polar dielectric in an external electric field
- Polar molecules have permanent dipole moment. The dipole moment of different molecules are randomly arranged in the absence of any external electric field.
- On applying the external electric field the dipole moment of these molecules tends to a lying along the field. Thus a net dipole moment is induced in the direction of field.
Electric Susceptibility
It is a measure of extent to which a material gets polarized when placed in an external electric field.
This is the required relation between electrical susceptibilty and dielectric constant.
Effect of Dielectric on Various Parameters
Let Qo, Co , Vo, Eo and Uo be the charge, capacitance, potential difference, electric field and energy stored respectively before the insertion of dielectric slab.
| When Battery is kept disconnected from the capacitor | When battery remains connected across the capacitor |
| Capacitance increases by K times; C = K Co | Capacitance increases by K times; C = K Co |
| Charge on the capacitor remains Qo | Potential difference remains constant, i.e., Vo |
| Electric Potential decreases by K times
|
Charge increases by K times
Q = CV = K CoV = K Qo |
| Electric field decreases by K times
|
Electric field remains constant
|
| Energy stored decreases by K times
|
Energy stored increases by K times
|
We would love your reading of Electric Charges and Fields, Electrostatic Potential and Capacitance, Magnetism and Matter, Electromagnetic Induction , Moving Charge and Magnetism, Current Electricity for scoring better and having deeper understanding of the chapters.
Do share the post if you liked Electrostatic Potential and Capacitance Class 12. For more updates, keep logging on BrainyLads