August 23, 2021

Magnetism and Matter Class 12 | Notes | Chapter 5 | Physics | CBSE |

Table of Contents

Magnetism and Matter Class 12 | Chapter 5 | Physics | CBSE |

Magnetism and Matter

A substance that attract pieces of iron or steel when suspended freely rests in south – North direction is known as Magnet.

A piece of iron or steel attains magnetic properties on rubbing with magnet and such type of magnets are commonly known as artificial magnets.

Some Basics of Magnetism

Magnetic poles always exist in pair . The poles of magnet can never exist freely, i.e., Magnetic monopoles do not exist. If we break a magnet, we find new poles formed at the broken end.
Like poles always repel each other and unlike poles always attract each other.
When a magnet is suspended freely with the help of a silk thread then it comes to rest in north south direction.
Earth also behaves as a magnet.
When a piece of material having some magnetic property is placed near a bar magnet. Then that material would acquire magnetism.
The force of attraction between two magnetic poles having strengths m₁ and m₂ and separated by a distance r is given as F = (μo / 4π) (m₁ . m₂ / r²)

Magnetic Field Lines

Space around a magnet in which its effect can be felt is defined as magnetic field.

Magnetic field line is an imaginary curve and tangent to which at any point gives the net direction of magnetic field at that point.

Properties of Magnetic Field Lines

Magnet field lines of a magnet form closed continuous loops. Outside the body of magnet, direction of field lines is from north to south.
Inside the magnet, direction of magnet field lines is from south to north.
No two magnetic field lines can intersect each other because if they intersect each other then there will be two direction of field which is not possible.
Magnetic field lines contract longitudnally
The magnitude of magnetic field at any point is directly proportional to number of magnetic field lines passing through that area.
At any point, tangent to the magnetic field lines gives the net direction of magnetic field.

Magnetic Dipole Moment

It is the product of strength of pole and magnetic length of the magnet. M = m (2 l)

Its SI unit is Ampere m²

Bar Magnet as an Equivalent Solenoid

Let a be radius of solenoid

i be strength of current passed through the solenoid

n be number of turns per unit length of solenoid

2 l be length of solenoid with centre O

We have to calculate magnetic field at point P on the axis of solenoid such that OP = r.

Consider a small element of width dx of a solenoid at a distance x from O

This is the required expression for magnetic field on the axial line of a short bar magnet. Hence, a finite solenoid carrying current is equivalent to bar magnet.

Electric Dipole Moment of a Revolving Electron or Bohr Magneton

Electrons revolves around nucleus in an atom. This revolving electron is like a loop of current with a definite dipole moment. If electron revolves in anticlockwise direction then electric current will flow in clockwise direction. Thus upper face of the electron loop behaves as south pole whereas lower face acts as north pole.

Let e be the charge on revolving electron and r be the radius of orbit

ω be the uniform angular velocity

Electric Current (i) = Charge (e) / Time (T)

Here T is the period of revolution of electron T = 2π / ω

i = e / (2π / ω) = eω / 2π

i = eω / 2π

Area of orbit in which electron is revolving, A = πr²

Magnetic moment of an atom is given as M = i A = (eω / 2π) ( πr² )

M = 1/2 eωr² ……(A)

According to Bohr’s postulate; m v r = nh / 2 π

m (ωr) r = n h / 2 π

ωr² = nh / 2 πm

Now Substituting the value of ωr² in equation (A), we get

M = (1/2) (e) (nh / 2 πm )

M = nhe / 4 πm

This is the required expression for orbital magnetic moment of an electron revolving in n^th orbit.

Bohr Magneton

It is defined as minimum magnetic dipole moment of an orbit due to motion of an electron in first stationary orbit (n = 1) of the atom.

e = 1.6 x 10^-19 C

h = 6.63 x 10^-34 Js

m = 9.1 x 10^-31 kg

μ_B = eh / 4 πm = 1.6 x 10^-19 x 6.63 x 10^-34 / 4 x 3.14 x 9.1 x 10^-31

μ_B = 9.27 x 10^-24 Ampere metre²

Gyromagnetic Ratio of Electron

It is the ratio of magnetic moment to the angular moment of an electron

Gyromagnetic Ratio = Magnetic Moment / Angular Moment = (1/2 eωr² ) / (mωr² )

Gyromagnetic Ratio = e / 2m = 8.8 x 10¹⁰ C / kg

Earth’s Magnetism

Question: What are the proof of earth’s magnetism?

Solution: Earth is itself a huge magnet because of the following evidences:

When a magnet is suspended freely with a thread and is allowed to rotate in horizontal plane it comes to rest along the north south direction.
When a piece of soft iron is buried under the earth, it is found to attain the properties of a magnet after sometime.
On plotting the magnetic field lines of a magnet, neutral points are obtained.

Concept: Earth’s crust has molten form of iron which contain charged ions. Earth rotates from west to east direction. Thus these charged ions produces a circulating current. The circulating current produced is mainly responsible for magnetic field of earth.

Some terms related to Earth’s Magnetism

Geographic Axis: The straight line passing through the geographic north and south poles of earth is defined as the geographic axis.

Magnetic Axis:The straight line passing through magnetic north and south poles of earth is commonly known as magnetic axis.

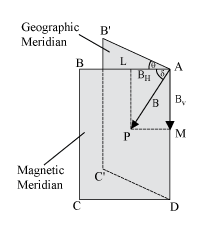
Geographic Meridian: The vertical plane passing through the geographic north and south poles is known as geographic meridian.

Magnetic Meridian: The vertical passing through the magnetic axis of freely suspended magnet is defined as Magnetic meridian.

Magnetic Elements of Earth

Magnetic elements of earth at any point are the quantities which gives the complete description about the magnitude and direction of magnetic field at that point.

There are three magnetic elements of earth as discussed below:

Magnetic Declination (θ)
Angle of dip or Magnetic inclination (δ)
Horizontal component (H) of earth’s magnetic field

Magnetic Declination (θ)

The angle between the geographic axis and magnetic axis at a place is defined as the magnetic declination at that point.

It is also defined as angle between magnetic meridian and geographic meridian at that place.

Angle of Dip or Magnetic Inclination (δ)

Magnetic dip or magnetic inclination at a place is defined as the angle which net earth’s magnetic field makes with horizontal in magnetic meridian.

Angle of dip is measured by a device commonly known as dip circle .

At equator, total magnetic field is parallel to horizontal, i.e., δ = 0

At earth’s magnetic poles δ= 90

Horizontal Component of Earth’s Magnetic Field

It is the component of net Earth’s magnetic field in horizontal direction. It is represented by H.

Earth’s magnetic field has a horizontal component only at magnetic equator.

At any point magnetic field can be resolved as horizontal component and vertical component

B_H = Bcos δ B_V = Bsinδ

Net Magnetic field, B = √ (B_H)² + (B_V)²

tan δ = B_V / B_H

Instrument used to measure horizontal component of earth’s magnetic field is commonly known as vibration magnetometer and a deflection magnetometer.

Special Cases

1. At Equator δ = 0°

B_V = B sin 0° = 0

B_H = B cos 0° = B

At equator vertical component of earth’s magnetic field is zero and only horizontal component exists.

2. At Pole δ = 90°

B_V = B sin90° = B

B_H = B cos 90° = 0

At a place on the magnetic pole, Horizontal component of earth’s magnetic field is zero and only vertical component exists.

Important Questions

Question : At what angle horizontal and vertical component of earth’s magnetic field have equal value?

Solution: B_H = B_V

B cosδ = B sinδ

tanδ = 1

δ = 45°

Question : Why does a compass become in effective in submarine?

Solution: The body of submarine is made of iron when a compass is kept in a submarine it experiences force from all side and thus the effective force on submarine becomes zero. Hence a compass becomes in effective in a submarine.

Question : Angle of dip at a place is 30°. Vertical component of Earth’s magnetic field at that point is 0.2 G. Calculate total magnetic field at that point.

Solution: B_V = B sin30°
0.2 = B (1/2)
B = 0.4 G
B = 0.4 × 10^-4 Tesla

Question : What will be the measure of vertical component of Earth’s Magnetic field at a point where dip is 60° and the horizontal component of earth’s magnetic field is 0.2 x 10^-4 T ?

Solution: tan 60° = B_V / B_H

B_V = √3 x 0.2 x 10^-4

B_V = 0.2√3 x 10^-4Tesla

We would love your reading of Electric Charges and Fields, Electrostatic Potential and Capacitance, Magnetism and Matter, Electromagnetic Induction , Moving Charge and Magnetism, Current Electricity for scoring better and having deeper understanding of the chapters.

Do share the post if you liked it. For more updates, keep logging on BrainyLads