Electric Charges and Fields Class 12 | Chapter 1 | Physics | CBSE |

Electric Charges and Fields Class 12 | Chapter 1 | Physics | CBSE |

Electric Charges and Fields

(I) Electrostatic Forces 

The branch of physics which deals with the study of charge at rest (i.e., static charges), the force between the static charges, field and potential due to these charges is called Electrostatics. 

Charge is something possessed by material object that make it possible for them to exert electrical force and  to respond to electrical force. It is basic unit of an existing body and charge at rest is present only on insulating rubbed surface and that too for very short period of time. 

Work function

1. It is the energy with which electron are bounded with metal surface .
2. It is measured in eV.
3. Greater the work function, more will be energy required to remove an electron from metal surface.
4. Platinum = Maximum work function
5. Cesium = Minimum work function 

Types of Charges 

Electron : -vely charged ; Mass = 9.1 x 10^-31 kg ; Charge = -1.6 x 10^-19 Coulomb  Proton : +vely charged ; Mass = 1.672 x 10^-27 kg ; Charge = + 1.6 x 10^-19 Coulomb  Neutron : Electrically neutral ; Mass = 1.674 x 10^-27 kg ; Charge = Zero 

Properties of Charge 

Additive Property

Additivity of charge is a property by virtue of which total charge of a system is obtained by simply adding algebraically all the charges present anywhere on the system. 

Note : Proper sign have to be used while adding the charges in a system

Conservation of Charge 

Conservation of charge is the property by virtue of which total charge of an isolated system always remain constant or conserved.  It is not possible to create or destroy net charge carried by any isolated system. 

Quantization of Electric Charge 

The quantization of electric charge is the property by virtue of which, the charge on a body is integral multiple of a basic unit of charge of an electron / proton represented by e.

q = ± ne

Here, n is any integer  The cause of quantization is that only integral number of electrons can be transferred from one body to another. 

Question: What is the charge on a body from which one million electrons are moved ?

Solution : n = 10⁶ , e = 1.6 x 10^-19 C 

As electrons are moved, charge acquired is positive 

q = ne = 10⁶ x 1.6 x 10^-19 C = 1.6 x 10^-13 C  

Charging 

The process of transferring of charge from one body to another body. 

Conduction 

The transfer of charge between two bodies by their actual contact.

Induction

The transfer of charge between two bodies without their actual contact.

Rubbing 

The transfer of charge between two bodies by rubbing them. 

Coulomb’s Law 

According to coulomb’s law, the force of attraction between any two bodies is directly proportional to the product of the charges and inversely proportional to square of distance between them. 

F = k | q₁ | | q₂ | / r² 

Here, k is electrostatic force constant. The value of electrostatic force constant depends on the nature of medium separating the charges, and on the system of units.

In SI Unit :    k = 9 x 10^-9 N m² C^-2

                         k = 1 / 4 π εo 

εo is electrical permittivity of the free space  

εo = 8.85 x 10^-12 N^-1 C² m^-2

Coulomb’s law is universal. The force which binds the electrons to the nucleus to form an atom is calculated from this law. It is Central Force as it acts along a line joining the two point two charges. It is a Conservative Force as the work is done in taking a charge from one point to another in the electric field of another charge is independent of path followed. It is not affected by presence or absence of any other charge. 

Dielectrics

These are kind of insulators which can conduct electricity when placed in external field. 

Dielectric Constant

Dielectric constant of a medium is the ratio of absolute electrical permittivity of the medium to the absolute electrical permittivity of free space. 

Dielectric constant of a medium may be defined as the ratio of force of interaction between two point charges separated by a certain distance in air / vacuum to the force of attraction / repulsion between the same two point charges, held the same distance apart in the medium. 

K = 1 for vacuum K = 1.003 ∼ 1 for air 

Question : Two point charges having equal charges separated by distance 1 m distance experiences a force of 8 N. What will be the new force experienced by them, if they are held in water at the same distance ? ( K _water = 80 )

Solution : F’ = F / K = 8 / 80 = 1 / 10 N 

Coulomb’s Law in Vector Form  

 

Let r ₁ be position vector of q₁ 

r ₂ be position vector of q₂

F₁₂ be force on q₁ due to q₂

F₂₁ be force on q₂ due to q₁ 

Thus, Coulomb’s Law is in accordance with Newton’s third law of motion. 

Force Between Multiple Charges : Principle of Superposition

According to Superposition principle; total force on any charge due to a number of other charges at rest is the vector sum of all the forces on that charge due to other charges, taken one at a time. The forces due to individual charges are unaffected by the presence or absence of other charges.

Question : A charge of magnitude Q is divided into two parts q and (Q-q) such that the two parts exert maximum force on each other. Calculate the ratio Q / q  

Solution: Force will be maximum only if dF / dq = 0

(1 / 4πεo) x d / dq [ q(Q-q) ] = 0

d / dq [ q(Q-q) ] = 0

q (-1) + (Q-q) = 0

Q – 2q = 0

Q = 2 q

Q / q = 2 

Question : Two identical metal spheres A and B have equal and similar charges. They repel each other with a force of 103 N, when they are placed 10 cm apart in a medium of dielectric constant 7. Determine the charge on each sphere.

Solution : F =  1 / 4 π εo / K q² r²

q = 28.6 x 10^-6 C 

Question :  Force between two electrical charges kept at distance d apart in air is F. If the distance between two charges is halved and their individual charges are doubled then new forces between them will become.

 

Force due to Continuous Distribution of Charges 

At the microscopic level, charge distribution is discontinuous as there are discrete charges separated by intervening space when there is no charge. 

Linear Charge Distribution

Total force due to continuous line distribution of charge is as follows 

 

 

     

 

 

 

Surface Charge Density

Total force due to continuous surface charge distribution is as follows

 

Volume Charge Density

By the superposition principle, total force due to entire volume charge density is obtained by summing over the forces due to different volume elements. 

        

(II) Electrostatic Field 

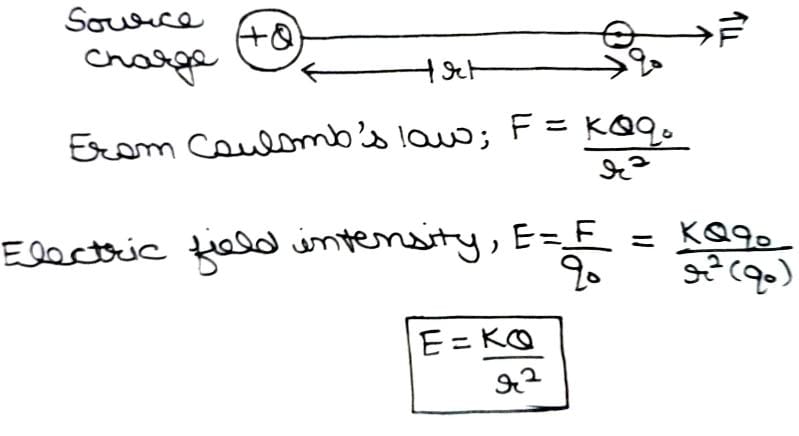
The Electric Field Intensity at any point is the strength of electric field at that point.

It is defined as the force experienced per unit positive charge placed at that point.

The charge Q which is producing the electric field is called a source charge and the charge qo which tests the effect of source charge is called a test charge.

Note : The test charge acts as detector of the electric field. It is an infinitely small charge so that it affects least the elctric field of source charge.

It is a vector quantity and direction of electric field intensity is along the direction of force. Its SI unit is N C^-1 

Electric Field Lines and Properties

An electric field line is a path, straight or curved in electric field, such that tangent to it at any point gives the direction of electric field intensity at that point. 

Electric Field Lines due to a point positive charge 

Electric Field Lines due to a point negative charge

Electric Field Lines due to an electric dipole

Electric Field Lines due to two equal positive charges

Electric Field Lines due to Positively charged plane conductor

Properties of Electric Lines of Force

1. Electric Field lines are continuous curves. They start from a positively charged body and end at a negatively charged body. 
2. Electric field lines are continuous but do not form closed loops.
3. Tangent to the electric field at any point at any point gives the direction of electric field intensity at that point.
4. No two electric field lines can intersect each other because if they intersect each other then there will be two direction of electric field which is not possible. Moreover, they are considered with same charge and same charge never intersect each other. 
5. The electric field lines are always perpendicular to the surface of a conductor.
6. The electric field lines contract longitudnally.
7. The electric field lines exert a lateral pressure due to repulsion between the charges.
8. Electric field lines travel from higher potential to lower potential. 
9. Electric field lines do not pass through conductor means inside a hollow conductor E = 0 
10. Closeness of electric field determines the strength of electric field. 

Electric Field Intensity due to a Point Charge

Let Q be source charge

q_o be a test charge 

r be the separation between source charge and test charge 

Electric Field intensity at a point depends only on source charge and separation between charge but not only on test charge

Electric Field Intensity on the Axis of Cicular Ring

Let a uniformly charged ring carrying charge q

R be radius of ring

We have to find electric field at point P which is at x distance from centre of ring

dq be small charge at ring which will produce dE electric field at point P. 

dE at point P can be resolved as dEsinθ and dEcosθ ; dEsinθ cancel each other and dEcosθ at point P gives total effect at point P. 

Special Cases:

When x = 0 i.e., at centre of ring E_net = 0

Distance when electric Field is maximum 

Electric Field intensity at centre due to circular arc

Electric Dipole

An electric dipole consists of a pair of equal and opposite point charges separated by some small distance. 

Dipole Length

The distance between the pair of charges or length of dipole is called as dipole length. 

Note : Total force and total charge due to an electric dipole is zero but electric field associated with a dipole is not zero. 

Dipole moment

Dipole moment is a measure of the strength of electric dipole. It is a vector quantity whose magnitude is equal to product of the magnitude of either charge and the distance between them. 

P = q x 2a 

By convention, the direction of P is from negative charge to positive charge. 

SI unit of dipole moment is Coulomb metre. 

Electric Field Intensity on Axial Line of an Electric Dipole 

Let AB be an electric dipole consisting of two point charge q and -q separated by a small distance 2a. We have to calculate electric field intensity E at a  point P on the axial line of the dipole and at a distance x from the centre of dipole 

Special Cases

1 ) If x >>> a; a² is neglected ( Very short dipole)

Enet = 2KPx / (x²)²  = 2 KP / x³ 

This is the required expression for electric field intensity on axial line due to short dipole 

2 ) If whole system is placed in a medium of dielectric constant (K)

E axial (medium) = Eaxial / K 

E axial (medium) = 2 KP / x³ / K 

Electric Field Intensity on Equatorial Line of an Electric Dipole 

Consider an electric dipole consisting of two point charges -q and +q separated by a small distance AB = 2a with a centre at O. 

We have to find electric field intensity E at point P on the equatorial line of the dipole OP = r

E can be resolved as Esinθ and Ecosθ

E_A sinθ and E_B sinθ cancel each other while E_A cosθ and E_B cosθ gives the net effect. 

E_Net = E_A cosθ + E_B cosθ

Special Case

If x>>> a ; a² is neglected 

When whole system of charges is placed in a medium whose dielectric constant is K

Eeq. _(medium) = Eeq. / K 

Relation between E_axial and E_eq. for a short dipole : 

Electric Field Intensity due to an Electric Dipole at some General Point

Consider an electric dipole consisting of two point charges -q and +q separated by a small distance AB = 2a with a centre at O.  

Let E₁ be field intensity on the axial line and E₂ be field intensity on equatorial point 

 

Torque Experienced by an Electric Dipole into a Uniform Electric Field

Let E be uniform electric field

P be Electric dipole moment

±q be pair of charges

2a be dipole length 

 

Torque = Force x Perpendicular displacement

Torque = ± qE x 2a sin θ

Torque = (q x 2a) E sin θ

Torque ; τ  = P E sin θ

Special Cases For Torque on an Electric Dipole

1) When Electric dipole is parallel to the electric field .i.e., P II E

θ = 0°

τ = PE sin 0°

τ = 0 (minimum)

2) When Electric dipole is perpendicular to the electric field 

θ = 90°

τ = PE sin 90°

τ = PE ( maximum )

3) When Electric dipole is anti-parallel to the electric field .i.e., P II E

θ = 180°

τ = PE sin 180°

τ = 0 (minimum)

Electric Potential Energy associated with an Electric Dipole placed in Uniform Electric Field 

Let θ1 be initial angle

θ2 be final angle

dθ be angular displacement 

Special Cases 

1) If θ₁ = 0° and θ₂ = θ

W = -PE [ cos θ₂ – cos 0]

W = -PE [ cos θ₂ – 1]

2) If θ₁ = 90° and θ₂ = 0°

W = -PE [ cos 0° – cos 90°]

W = -PE (1)

W = -PE (Minimum energy) (Stable condition ) 

3) If θ₁ = 90° and θ₂ = 180°

W = -PE [ cos 180° – cos 90°]

W = -PE (-1)

W = PE (Maximum energy) (Unstable condition ) 

Question : Calculate the amount of work done required to rotate an electric dipole from stable to unstable condition into a uniform electric Field. 

Solution : W = -PE [ cos θ₂ – cos θ1 ]

In stable condition ; θ1 = 0°

In Unstable condition ; θ2 = 180°

W = -PE [ cos 180° – cos 0°]

W = -PE [-1-1]

W = 2 PE 

Question : An electric dipole of length 2 cm when placed with its axis making an angle of 60° with a uniform electric field experiences a torque of 8√3 N m. Calculate the potential energy of the dipole if it has a charge of ± 4 nC. 

Solution : Length (2a) = 2 x 10^-2 m

Angle, θ = 60°

Torque = 8√3 Nm 

Charge = 4 x 10^-9 C

We know; τ = Q (2a)  E sinθ

E = 8√3 / 4 x 10^-9  x 2 x 10^-2  x sin 60°

E = 2 x 10 ¹¹ N C^-1

Now; U = -PE cosθ = – 4 x 10^-9  x 2 x 10^-2  x 0.5 x 2 x  10 ¹¹  = – 8 J 

Question : Two point charges of ±3.2 x 10^-19 C separated by 2.4 x 10^-10 m . The dipole is placed in a uniform electric field of 4 x 10⁵ N C^-1. Calculate work done in rotating dipole by 180°. 

Solution : q = ± 3.2 x 10^-19 C 

E = 4 x 10⁵ N 

2a = 2.4 x 10^-10 m

We know; work done in rotation the dipole = 2 PE 

U = 2 x 3.2 x 10^-19 x 2.4 x 10^-10 x 4 x 10⁵

U = 61.44 x 10^-24 J 

Force associated with an Electric Dipole in Non Uniform Electric Field

Let ±q be pair of charges 2a be dipole length 

 

 (III) Electric Flux

Area Vector

By convention , the vector associated with every area element of a closed surface is taken to be in the direction of the outward drawn normal. 

Electric Flux 

Electric flux over an area in an electric field is measure of the number of electric field lines crossing this area.

Electric Flux is a scalar quantity. Electric flux over a closed surface can be positive, negative or zero.

Its SI unit is Nm²C^-2 

Dimensional formula of Φ_E is [ML³T^-3A^-1] 

Gauss’s Law

The surface integral of electric field E produced by any source over any closed surface S enclosing a volume V in vacuum i.e., total electric flux over a closed surface S in vacuum is 1 / εo times the total charge (Q) contained inside S. 

Note : There is no contribution to electric flux from the charge outside S. Further, the location of Q inside S does not affect the value of surface integral.

The charge inside S may be point charge or even continuous charge distribution. The surface chosen to calculate the surface integral is called Gaussian surface. 

Proof of Gauss’s theorem (For spherically symmetrical surfaces only)

Suppose an isolated positive point charge is situated at centre O of a sphere of radius r. 

Note: Electric Flux does not depend on shape of surface but it depends on the charge placed inside the closed body. Moreover, the surface need not to be a real physical surface; it can also be a hypothetical one. 

Some Important cases related to Gauss’s law

	Φin = -πR2E  Φout = πR2E            Φtotal = 0
	Φin = Φcircular = -πR2E  Φout = Φcurved  = πR2E  Φtotal = 0
	Φin = -1/2 πR2E  Φout = 1/2 πR2E Φtotal = 0
	Note : Here Electric Field is radial Φ = q / 2 εo

Φ = q / 2 εo

Electric Flux for a Cube at Different Locations

If a charge is at centre of cube 

io

Φ_Total = Q / εo 

Φ_Face = Q / 6 εo

Φ_Corner = Q / 8 εo 

Φ_Edge = Q / 12 εo     

Question: A surface S₁ of radius r₁ encloses in a charge Q. If there is another concentric sphere S₂  (r2 > r1) enclosing charge 2Q. Find the ratio of electric flux through S₁ and S₂. How will the electric flux through sphere S₁ change if a medium of dielectric constant K is introduced in the space inside S₂ in place of air?

Solution: According to Gauss’s law;
Flux through S₁ = Q / εo
Flux through S₂ = Q + 2Q / εo
On dividing equation (i) by equation (ii) , we get
Φ₁ / Φ₂ = 1 / 3
There is no change in electric flux through S₁ with dielectric medium inside the spare S₂.

Deduction of Coulomb’s Law from Gauss’s Law

Consider an isolated positive point charge q at O. Imagine a sphere of radius r with centre O. The magnitude of electric field intensity E at every point on the surface of the sphere is the same and it is directed radially outwards. Further, the direction of vector ds representing a small area element ds on the surface of the sphere is along E only, i.e., θ = 0°. 

This is the electric field intensity at point P distant r from an isolated point charge q at the centre of the sphere. If another point charge q_o were placed at P, then force on q_o would be 

This is Coulomb’s Law

Important Application of Gauss’s Theorem

Electric Field Intensity due to an Infinitely Long Straight Wire

Consider an infinitely long thin wire with uniform linear charge density λ. In order to find electric field at distance r from it; there is a gaussian surface. 

This cylinder has four surfaces. 1,4 are plane surfaces and 2,3 are curved cylindrical surfaces. 

Let Φ1, Φ2, Φ3 , Φ4 are flux associated at 1,2,3,4 surfaces. 

L be length of cylinder upto gaussian surface. 

Electric Field Intensity due to uniformly charged Spherical Shell

Consider a thin spherical shell of radius R with centre O. Let a charge +q be distributed uniformly over the surface of the shell. The surface of this sphere is Gaussian surface at every point of which electric field intensity E is the same, directed radially outwards

Electric Field Intensity at a point outside the shell ( r > R)

Electric Field Intensity at a point on the surface of shell ( r = R)

Electric Field Intensity at a point inside the shell

We know, in case of spherical shell; no charge exists inside the gaussian surface i.e., E = 0 

Variation of Electric Field Intensity (E) with distance (r) from the centre O of a charged spherical shell

Electric Field Intensity due to a Non – Conducting Charges Solid Sphere

Suppose, a non conducting solid sphere of radius R and centre O has uniform volume density of charge ρ. 

 Electric Field Intensity at a point outside the solid sphere ( r > R ) 

Draw a gaussian surface in the form of a sphere of radius r with O as centre. From Gauss’s law ; 

Electric Field Intensity at a point on the surface of solid sphere ( r = R)

Electric Field Intensity at a point inside the solid sphere

Draw a gaussian surface of radius r with O as same charge enclosed by gaussian surface

Variation of Electric Field Intensity (E) with distance (r) from the centre O of a non conducting  charged solid sphere

Electric Field Intensity due to Thin Infinite Plane Sheet of Charges 

Consider a thin infinite plane sheet of charge. Let σ be the surface density of charge on the sheet. 

From symmetry, we find that E on either side of the sheet must be perpendicular to the plane of the sheet, having the same magnitude at all points equidistant from the sheet. 

Let us imagine a cylinder of cross sectional area ds piercing through the sheet. 

If the sheet carries positive charge, σ > 0. The electric field is uniform , normal and outwards from the sheet. If the sheet carries σ < 0 ; the field is uniform and along the inward normal to the plane sheet. 

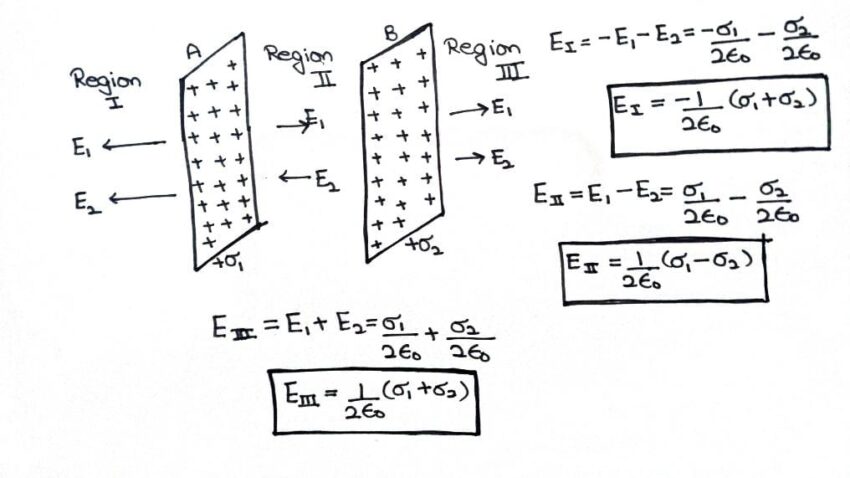
Electric Field Intensity due to Two Thin Infinite Plane Parallel Sheets of Charges

Let A and B be two infinite plane charged sheets held parallel to each other. 

σ₁ = Uniform surface density of charge on A

σ₂ = Uniform charge density of charge on B 

Question : A hollow cylindrical box of length 1 m and area of cross section 25 cm² is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by E = 50 xî, where E is in NC^-1 ans x is in metre. Find net electric flux through the cylinder.

 

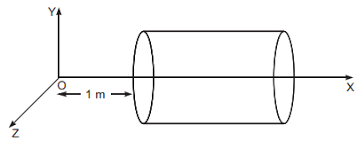
Solution : Given, E = 50 xî

As the flux is only along the X axis, so flux will pass only through the cross sectional area of the cylinder

Magnitude of electric field at cross section A, E_A = 50 x 1 = 50 N C^-1

Magnitude of electric field at cross section A, E_B = 50 x 2 = 100 N C^-1

The corresponding electric fluxes are

Φ_A = E_A. ΔS = 50 x 25 x 10^-4 x cos 180° = -0.125 Nm²C^-1

Φ_B = E_B. ΔS = 100 x 25 x 10^-4 x cos 0° = 0.25 Nm²C^-1

So net flux through the cylinder, Φ = Φ_A + Φ_B =-0.125+0.25 

Φ = 0.125 Nm²C^-1 

Question : Given a uniform electric field E = 5 x 10³ î NC^-1, find the flux of this field through a square of 10 cm on a side whose plane is parallel to YZ plane. What would be flux through the same square if the plane makes an angle of 30° with X axis.

Solution: Given; electric field intensity = 5 x 10³ î NC^-1

Side of square, S = 10 cm = 0.1 m

Area of square = (0.1)² = 0.01 m²

The plane of this square is parallel to YZ plane. Hence, the angle between the unit vector normal to the plane and electric field is zero i.e., θ = 0°

Flux through the plane, Φ = E.A cosθ = 5 x 10³ x 0.01 cos 0° = 50 Nm²C^-1

If the plane makes an angle of 30° with X axis then  θ = 60°

Flux through the plane, Φ = E.A cosθ = 5 x 10³ x 0.01 cos 60° = 25 Nm²C^-1

We would love your reading of Electric Charges and Fields, Electrostatic Potential and Capacitance, Magnetism and Matter, Electromagnetic Induction , Moving Charge and Magnetism, Current Electricity for scoring better and having deeper understanding of the chapters.

Do share the post if you liked the notes of Electric Charges and Fields Class 12. For more updates, keep logging on BrainyLads