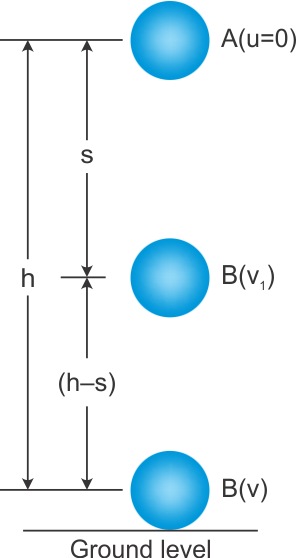Work Energy and Power Class 9 | Science | Notes | Term 2 |

Work Energy and Power Class 9 | Science | Notes | Term 2 |

Both work and energy concepts are closely correlated. When we walk or run then we use the energy that we get from the food we eat. The concept of power is also closely associated with that of work.

Work

When a force applied on a body causes the displacement in the body of the object then the work is said to be done. In order to say that the work is done the conditions which must be satisfied are as follows:

• Force must act on the body
  
• The body must undergo displacement from one position to another position.
  

Joule is considered as the SI unit of work.
It is a scalar quantity.

W = F × s
Work is said to be 1 joule when a force of 1 Newton displaces the object by a distance of 1 metre.

Positive and Negative Work Done

When displacement of an object is in the direction of force applied then the work done is said to be positive.
When displacement of an object is in the opposite direction of that a force applied then the work done is said to be negative.

Energy

It is simply the ability to do work. The amount of energy possessed by a body is numerically equal to the amount of work it can do when the energy is released.
It is a scalar quantity.
It is a unit same as that of work, i.e., Joule.
1 KJ = 1000 Joules
Various forms of energy are kinetic energy, potential energy, solar energy, mechanical energy, chemical energy, light energy and so on.

Kinetic Energy

It is the energy of a body that is possessed by it due to its motion.
Every object around us which has speed possesses kinetic energy. The amount of work UK body can do before coming to rest helps in measuring the kinetic energy of the moving body. It varies directly proportional to the speed
v² – u² = 2aS
S = v² – u² / 2a

We know, W = F × S
Substituting the value of S, we get
W = (ma) ( v² – u² / 2a )
W = 1/2 m × v² – u²
E_k = 1/2 m × v² – u²

If the object starts from rest then u = 0
Therefore, E_k = 1/2 m × v²

Potential Energy

The energy which is attained by a body by virtue of its position or configuration. In order to lift a body above the surface of earth we have to do a work against the force of gravity.
Therefore, Work = Force × displacement
W = mgh
P.E = mgh

Example: water stored in an overhead tank possesses gravitational potential energy by virtue of its position.

Law of conservation of Energy

As per this law energy can neither be created nor be destroyed but it can be changed from one form to another form. Since this law holds universally thus it is valid in all situations and for all kind of transformations.

Verification of law of conservation of energy is as follows:
Let m be the mass of the body held at position A and h be height above the ground.

At position A
Kinetic energy of body will be zero since the body is at rest position A.
Potential energy of the body at A, PE = mgh
Total mechanical energy = 0 + mgh = mgh
M.E_A = mgh
Now let the body be allowed to fall freely under the action of gravity. In the case of free fall and the body reach the point B with velocity v₁ where AB = s

At position B
v² – u² = 2as
V₁² = 2gx
Thus, Kinetic energy of body= 1/2 m V₁²
K.E = 1/2 m (2gs) = mgs
K.E= mgs
Height of the body be above the ground will be h-s
Total mechanical energy at position B = mgs + mg(h-s) = mgh
M.E_B = mgh

At position C
v² – u² = 2as
V² = 2gh
Thus, Kinetic energy of body= 1/2 m v²
Substituting the value of v²
K.E = 1/2 m (2gh) = mgh

Potential energy of the body at position C = 0
Hence total mechanical energy of the body at position C = mgh + 0 = mgh
M.E_C = mgh

Now as we observe the total mechanical energy remains constant at each point of motion of the freely falling body. This proves the law of conservation of mechanical energy.

Power

The rate of doing work is simply defined as the power. It can also be defined as the rate at which energy is transferred by an object.
Watt is considered as the SI unit of power.
It is a scalar quantity.
If a bulb has 9 watt reading, this means that bulb consumes 9 joule energy per second.
Greater the power of an appliance and the longer it is switched on the more electrical energy it consumes.

Commercial Unit of Energy

Kilowatt hour is the commercial unit of energy. Joule is quite a smaller unit and is inconvenient in order to express large quantities of energy.
1 KWh = 3.6 × 10⁶ Joule
Kilowatt hour is also known as unit.
Electrical energy consumed during a month is expressed in terms of units

Questions / Answers of Work, Energy and Power

Question 1: How work is done by a force of 20 Newton in moving an object through a distance of 1 metre along the direction of the force?

Answer: We know, Work done = Force × displacement
W = 20 × 1 = 20 J
Thus 20 Joule of work is being done.

Question 2: If a work of 4900 Joule is done in order to lift a mass of 50 kg to a certain height. Determine the height through which the load is lifted.

Answer: We know, Work done = Force × displacement
4900 = 50 × h
h = 98 metre

Question 3: How will the kinetic energy of a body change if the velocity of the body is doubled?

Answer: We know, E_k = 1/2 mv²
Thus if velocity is doubled
v’ = 2v
E_k‘ = 4 E_k
This kinetic energy becomes 4 times of its original kinetic energy.

Question 4: Two bodies having equal masses move with uniform velocities v and 2v respectively. Determine the ratio of their Kinetic energies.

Answer: The ratio of their kinetic energy is will be 1 : 4 since kinetic energy varies directly proportional to square of velocities.

Question 5: Give give few example in which case the object is not displaced in spite of the force applied on it.

Answer: Following are the examples wherein force is being supplied supplied and still there is no displacement:

• A rigid wall being pushed by a man.
  
• A boy carrying a basket on his head and standing steady. In such case the force of gravity acts on the basket but the displacement is zero.
  
• A stationary truck being pushed by a man.

Question 6: Give one example of the case where in the mass of the body is small but the kinetic energy is high.

Answer: A cricket ball which has been hit hard and is travelling fast is the suitable example of the given case.

Question 7: Determine the power consumed by a pump that takes 10 second in order to lift 100 kg of water tank situated at a height of 20 metre?

Answer: Power = Work / Time
Power = 100 × 10 × 20 / 10 = 2000 Watt
Hence, 2000 watt of energy is consumed.

Question 8: An electric iron of power 1200 watt is used for 30 minutes daily. Determine the electrical energy consumed in the month of April?

Answer: Power = 1200 / 1000 = 1.2 kW
Time = 30 / 60 = 0.5 hour
Electric energy= Power × time × days
Electric energy= 1.2 × 0.5 × 30
Electric energy= 18 kWh

Question 9: Determine whether the work is said to be done or not when a donkey is carrying a load on its back.

Answer: In the case, when the displacement of an object is perpendicular to the force acting on it, then the work done by the force on the object is considered zero.
In the given situation the force of gravity on the load is acting vertically downward whereas the displacement is in horizontal direction. We can say that the force and displacement are perpendicular to each other. Hence there is no displacement in the direction of force of gravity as a result work done is zero. 

# Work, Energy and Power Class 9 Science Notes

# Work Energy and Power Class 9

Do share this post if you liked Work, Energy and Power Class 9 Science Notes. For more updates, keep logging on BrainyLads.