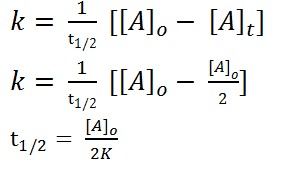June 28, 2021

Chemical Kinetics Class 12 Notes | Chapter 4 | Chemistry | CBSE |

Table of Contents

Chemical Kinetics Class 12 Notes | Chapter 4 | Chemistry | CBSE |

Chemical Kinetics

Chemical Kinetics Class 12 Notes : Chemical Kinetics is the branch of chemistry which deals with speed or rate of chemical reaction . It also explains factors affecting rate of chemical reaction . It also describe the condition by which the reaction rates can be varied.

Some reactions such as ionic reaction occur very fast ( takes place in 10^-12 to 10^-16 sec) . Ex: Precipitation of silver chloride.
On the other hand , some reaction takes place very slow . Ex: Rusting of iron in presence of air and moisture.
Some reaction proceed with moderate speed like inversion of cane sugar.

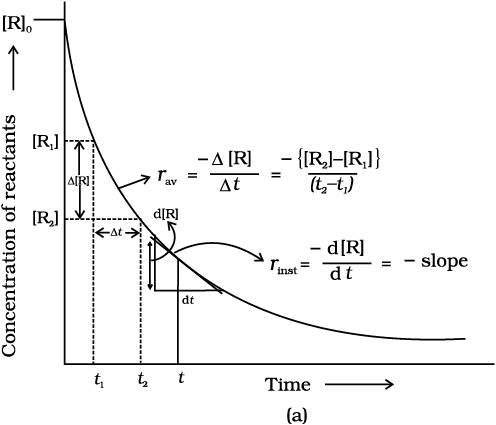
Average Rate of Reaction

It is defined as decrease in concentration of reactant or increase in concentration of product per unit time . It is not constant throughout the reaction .

Average Rate of Reaction = Dec. in concentration of Reaction / Time Interval

Average Rate of Reaction = Inc. in concentration of Reaction / Time Interval

Δt = t₂ – t₁ Δ[R] = R₂ – R₁ Δ[P] = P₂ – P₁

The square brackets are used to express molar concentration.

Rate of disappearance of R = – Δ[R] / Δt ; -ve sign is used as conc. of reactant dec. with rxⁿ

Rate of appearance of P = Δ[P] / Δt

Units of Rate of Reaction

If concentration is in mol L^-1 and time is in second. Its unit will be mol L^-1 s^-1 .
In gaseous reaction , if concentration is in partial pressure and time is in sec. then unit of reaction will be atm s^-1 .

To express the rate at a particular moment of time we determine instantaneous rate.

Now , consider a reaction Hg + Cl₂ → HgCl₂

When stoichiometric Coefficient of reactant and product are same , rate of reaction is expressed as

2HI → H₂ + I₂

For expressing rate of reaction where stoichiometric coefficient are not same , rate of reaction is equal to rate of disappearance of reactant or appearance of product divided by its stoichiometric coefficient .

Note : For a gaseous reaction at constant temperature , concentration is directly proportional to partial pressure of species and rate can also be expressed as rate of change in partial pressure of reactant or the product.

Ques : 2NO₂ + F₂ → 2NO₂F Express the Rate of Reaction

Sol :

Factors Affecting Rate of Chemical Reaction

1) Concentration of Reactant : Rate of reaction ∝ [Reactant] ; Initially , rate of reaction will be high after sometime it starts to decrease.

2) Temperature : Rate of reaction ∝ Temperature (but no of collision also increase)

3) Presence of Catalyst : Catalyst enhance rate of reaction

4) Surface Area : Rate of reaction ∝ surface area ; Reactant should be taken in powdered form as smaller is the particle size i.e greater is the surface area ; faster is the reaction.

Dependence of Rate on Concentration

Law of Mass Action

The rate of reaction is directly proportional to product of molar concentration of reacting species each raised to power their stoichiometric coefficient at a given temperature .

a A + b B → Product

Rate of Reaction ∝ [A]^a [B]^b

Rate of Reaction = k [A]^a [B]^b

Here K is rate constant or velocity constant or specific reaction rate .

Characteristics of Rate Constant

Rate of reaction depends upon rate constant . As the value of rate constant increases , rate of reaction also increases.
Each reaction has fixed value of K at a fixed temperature .
For the same reaction , value of K changes with change in temperature .
K is independent from concentration , pressure and volume of reactant.

Rate Law for a Chemical Reaction

The expression which describes the reaction rate in terms of molar concentration of reactants as determined experimentally is called rate law .

2NO₂ + F₂ → 2NO₂F

According to law of Mass Action : Rate of reaction = k [NO₂]² [F₂]¹

According to Rate Law Expression : Rate of reaction = k [NO₂]^α [F₂] ^β

α and β are experimentally verified coefficient and actual coefficient .

Num : For the reaction A + B → Product

rate law expression for rate = K [A]¹[B]² If volume of the vessel is reduced to 1/3 of its original volume then what will be the effect on rate of reaction ?

Solⁿ : rate = K [A]¹[B]²

by reducing the volume to 1/3 of its original volume then concentration of reactant will be 3 times rate of reaction = K [3A]¹[3B]²

rate of reaction = 27 × K [A]¹[B]²

Rate of reaction will become 27 times to its initial value .

Order of Reaction

The sum of coefficient of reacting species that are involved in rate law expression

a A + b B → Product

Accoding to rate law expression : Rate of reaction = k [A]^α [B] ^β

order of reaction = α + β

First Order Reaction

A reaction is said to be first order if rate of reaction depend only upon one concentration term .

A → Product Rate of reaction = k [A]¹

NH₄NO₂ → NO₂ + 2H₂O Rate of reaction = k [NH₄NO₂]

Second Order Reaction

Dissociation of 2HI → H₂+ I₂ Rate of reaction = k [HI]²

Reaction between NO and O₃NO + O₃ → NO₂ + O₂ Rate of reaction = k [NO]¹ [O₃]¹

Third Order Reaction

Combination of NO and O₂ to form NO₂ 2NO + O₂ → NO₂ Rate of reaction = k [NO]² [O₂]¹

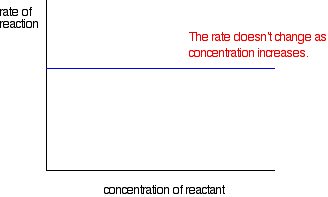
Zero Order Reaction

Its rate is independent of concentration of reacting species . It involves presence of catalyst , sunlight , UV , gaseous reaction with pt under high pressure.

Fractional Order Reaction

Reaction b/w H₂ and Br₂ to form HBr H₂ + Br₂ → 2HBr

Rate of Reaction = k [H ₂]¹ [Br₂]^1/2 order = 3/2

Unit of Rate Constant

n A → Product

Rate = K [A]ⁿ = K [ mol L^-1 ]ⁿ

K = Rate / [mol L^-1]ⁿ K = [mol L^-1]^1-n s^-1

here n is order of reaction

Reaction	order	Unit of rate constant
Zero order reaction	0	mol L^-1s^-1
First order reaction	1	s^-1
Second order reaction	2	mol^-1 L s^-1

Elementary Reaction

The reaction which takes place in single step is called elementary reaction OR the chemical reaction which involves no intermediate.

NH₄NO₂ → N₂ + H₂O

Complex Reaction

The reaction which takes place in more than one step is called Complex reaction OR The reaction which involves one or more intermediate .

4HBr + O₂ → 2H₂O + 2Br₂

Molecularity of Reaction

The number of reacting species taking part in a chemical reaction that must collide simultaneously in order to bring about a chemical reaction is called molecularity of reaction.

Unimolecular Reaction

The reaction which has value of molecularity one . NH₄NO₂ → N₂ + H₂O

Bimolecular Reaction

The reaction which has value of molecularity two . 2HI → H₂+ I₂

Trimolecular Reaction

The reaction that involve simultaneous collision between three reacting species

2NO + O₂ → NO₂

The probability that more than three molecules can collide and react simultaneously is very small . Hence , reaction with molecularity three are very rare and slow to proceed.

Note : In a complex reaction, overall rate of reaction is controlled by slowest step in a reaction called the rate determining step.

Order of Reaction	Molecularity of Reaction
It is an experimental quantity , it can be zero and even a fraction .	It cannot be zero or a non integer .
It is applicable to elementary as well as complex reaction .	It is applicable only for elementary reaction .
For complex reaction , order is given by slowest step .	Molecularity of the slowest step is same as the order of overall reaction .

Determination of Order of Reaction

1) Initial Rate Method

This method is used when more than one reactant are present in a reaction.

Numerical : A + B → Product

Experiment	Initial Concentration [A]	Initial Concentration [B]	Intial Rate (mol L^-1s^-1 )
1	0.10 M	1.0 M	2.1 × 10^-3
2	0.20 M	1.0M	8.4 × 10^-3
3	0.20 M	2.0 M	8.4 × 10^-3

Determine the order of reaction w.r.t A and B and overall order of reaction ?

Solⁿ : Acc to rate law expression : Rate of Reaction = k [A]^α [B]^β

Experiment 1 r₁ = K [0.10]^α [1.0]^β …(i)

Experiment 2 r₂ = K [0.20]^α [1.0]^β …(ii)

Experiment 3 r₃ = K [0.20]^α [2.0]^β …(iii)

divide equation (ii) by (iii) ; r₂ / r₃= K [0.20]^α [1.0]^β / K [0.20]^α [2.0]^β

r₂ / r₃= [1.0]^β / [2.0]^β

8.4 × 10^-3 / 8.4 × 10^-3 = [ 1/ 2 ]^β

1 = [ 1/ 2 ]^β

β = 0

divide equation (ii) by (i); r₂ / r₁ = K [0.20]^α [1.0]^β / K [0.10]^α [1.0]^β

8.4 × 10^-3 / 2.1 × 10^-3 = [ 2 /1]^α

α = 2

Thus , order w.r.t A is 2

Thus , order w.r.t B is 0

overall order of reaction is 2

Rate law expression is k [A]² [B]⁰

2) Integrated Rate Law Method

Integrated rate equation for Zero order reaction

Rate of reaction = – Δ [A] / Δt

Rate of reaction = K [A]^o

– Δ [A] / Δt = K [A]^o

– Δ [A] = K Δt

Integrating Both Sides

[A] = – K t + I

at t = 0 , [A]_t = [A]₀

[A]₀ = − K × 0 + I

I = [A]₀

[A]_t = – K t + [A]₀

K t = [A]₀– [A]_t

Graphs for Zero Order Reaction

i) Plot of [A] vs time

[A]_t = – K t + [A]₀

y = mx + c { m = – K }

ii) Rate vs Concentration of Reactant

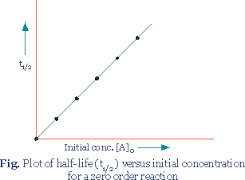
Half Life Period for Zero Order Reaction ( t_1/2 )

Half life period is the time in which half of the reaction is completed or half of the substance has reacted

at t = 0 initial concentration = [ A ]_O at t = t_1/2 concentration will be [ A ]_O / 2

{ y= mx + c} { here, c = 0}

Integrated Rate Equation for First Order Reaction

A → Product

at t = 0 initial concentration = [A]₀

at t = t concentration will be [A]_t

Rate of reaction = – Δ [A] / Δt Rate of reaction = K [A]¹

– Δ [A] / Δt = K [A]¹

– Δ [A] / [A]¹ = K Δt

Integrating Both Sides

-ln [ A] = kt + I

At t = 0 , A = [A] ₀

– ln [A] ₀ = 0 + I

I = – ln [A] ₀

–ln [A] _t = K t – ln [A] ₀

K t = ln [A] ₀–ln [A] _t

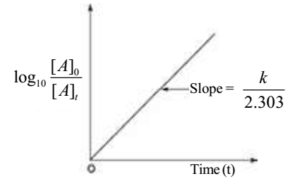
Plot of log₁₀[A]_t with Time

K t / 2.303 = log ₁₀ [A] ₀– log ₁₀ [A] _t

log ₁₀ [A] _t= – K t / 2.303 + log ₁₀ [A] ₀

Slope = – K / 2.303

Plot of log 10 ( [A] ₀ / [A]_t ) with Temperature

Half Life Period for First Order Reaction ( t_1/2 )

at t = t_1/2 concentration will be [ A ]_O / 2

t_1/2 = (2.303 / K ) log ₁₀ 2

t_1/2 = 0.693 / K

Integrated Rate Equation for First Order Reaction in Gaseous Phase .

A_(g)→ C_(g) + D_(g)

At t = 0 P_i(atm) 0 0

At t = t P_i – x x x

Pressure at time t = P_i – x + x + x

x = P_t – P_i

Num : A first order reaction is 50% complete in 25 min. Calculate time for completion for 80% of the reaction ?

Pseudo Chemical Reaction

In certain chemical reaction , experimentally determined order is different from what it is expected . Such chemical reaction is called Pseudo Chemical Reaction . Ex : Hydrolysis of ester

CH₃COOC₂H₅ + H₂O → CH₃COOH + C₂H₅OH

The concentration of water does not get much altered during the reaction since Ethyl acetate is in excess .

Inversion of cane sugar is another example of pseudo first order reaction .

C₁₂H₂₂O₁₁ + H₂O → C₆H₁₂O₆ + C₆H₁₂O₆

Rate = k [C₁₂H₂₂O₁₁]

Temperature Dependence of the Rate

The rate of reaction is dependent on temperature. This is expressed in terms of temperature coefficient. Most chemical reaction are enhanced / proceeded with increase in temperature . Example : In a mixture of oxalic acid and potassium permanganate , potassium permanganate gets decolourised faster at high temperature .

Temperature Coefficient

It is the ratio of rate constant at temperature 308 ( 298+10) K to the rate constant at temperature 298 K

Temperature Coefficient = Rate constant at 308K / Rate constant at 298 K

Note : It is observed that for a chemical reaction with rise temperature by 10⁰ , the rate constant is nearly doubled.

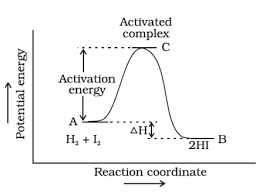
Arrhenius Equation

Quantitatively , the effect of temperature on the rate of reaction and hence on the rate constant was proposed by Arrhenius . The equation called Arrhenius equation is as follows :

k = A . e ^{–Ea / RT}

where the pre-exponential factor A is constant and is called frequency factor .

E_a is the energy of activation , R is gas constant and T is the absolute temperature.

Arrhenius Theory

Arrhenius theory states that product are formed through the intermediated or activated complex .

H₂ + I₂ → 2HI

intermediate is unstable and exists only for a very short time .

The factor e ^{–Ea / RT} gives the fraction of molecules (N_E / N_T ) having energy equal to or greater than activation energy , where N_E represents number of molecules with energy E and N_T represents total number of molecules .

k = A . e ^{–Ea / RT}

^{Taking natural logarithm on both sides}

^{ln K = –Ea / RT + ln A}

^{now slope = –Ea / RT and intercept is ln A}

^{Now ,at temperature T₁ ; ln K = –Ea / RT₁ + ln A}

^{At temperature T₂ ; ln K = –Ea / RT₂ + ln A}

^{subtracting equation (b) from (a) , we get}

^{Activation Energy}

^{It is given by the energy difference between activated complex and the reactant molecules. It is the energy needed to form the intermediate called activated complex or it is the extra energy contained by the reactant molecules that results into effective collision between them to form the products.}

Effect of Catalyst on the Rate of Reaction

Catalyst is a substance which change the speed of reaction without itself undergoing any chemical change .
Effect of catalyst can be understand by intermediate complex theory which states that reactant first combine with catalyst to form an intermediate complex which is short lived and decomposes to form product and regenerating the catalyst .
A catalyst does not alter free energy change (ΔG ) of a reaction .
It catalyses only spontaneous reaction .
A catalyst cannot initiate a reaction . It can only accelerate the rate of reaction .
It does not affect equilibrium constant and enthalpy change (ΔH ) of the reaction .

Collision Theory of Chemical Reaction

The number of collision that takes place per second per unit volume of the reacting mixture is called collision frequency (Z) .
At ordinary temperature and pressure, the value of collisions frequency is so high (10² to 10⁵ in a gaseous reaction) that if all the collisions were effective, i.e result into chemical reaction, the reaction should be completed in the fraction of a second. However, in actual practice, this is not so. This is explained as follows :
For a collision to be effective, the colliding molecules must have energy more than a particular value i.e threshold energy.
For a bimolecular elementary reaction A + B → Product rate = Z_AB e ^{–Ea / RT} here , Z_AB represents collision frequency
The collisions that leads to breaking of bond between reaction species and formation of new bonds to form product are called as effective collision .
To account for proper effective collision of reactant molecule ; proper orientation of reactant molecule is necessary as it leads to bond formation otherwise molecule will bounce back . This is called P probability factor OR orientation factor OR steric factor . Thus , Rate = P Z_AB e ^{–Ea / RT}
Limitation : Collision theory assumes atoms or molecules to be hard spheres and does not take into account their structural aspect.

# Chemical Kinetics Class 12 Notes

# Chemical Kinetics Class 12 Notes in Brief

# Chemical Kinetics Class 12 Notes & NCERT Solutions

# Chemical Kinetics Class 12 Notes Elaborated

Do share the post if you liked Chemical Kinetics Class 12 Notes. For more updates, keep logging on BrainyLads