Foreign Exchange Rate Class 12 | Demand and Supply | Curve |
Table of Contents
Foreign Exchange Rate Class 12 | Demand and Supply | Curve | Chapter 11 |
What is Foreign Exchange of Foreign Exchange Rate?
Foreign Exchange Rate Class 12 : Foreign exchange refers to the currency other than domestic currency or the currencies of all the rest of countries other than the domestic one.
Foreign exchange rate refers to the rate at which one unit of foreign currency can be purchased by giving domestic currency or it refers to the rate of other currencies (rest of the world) in terms of domestic currency.
As per Crowther, “The rate of exchange measures number of units of one currency which is exchanged in the foreign market for one unit of another.”
Why is Foreign Currency needed?
The need (demand) of foreign currency is due to following factors which are as follows:
- Payment of Import of Goods and Services: When the goods or services are imported from other country. In that case, the payment is made in the form of foreign currency due to which a person needs foreign currency for the payment of goods and services which are imported.
- Investing in other Country: When a person wants to invest his amount in the other country in that case he also needs that country’s currency for investment purpose.
- Repayment of Loans: The loans which are taken from other or foreign countries are repaid in their currency for which currency of their country is needed.
- Tourism: A person needs foreign currency for the expenditure in other country.
- Income Payment: Forex is required to pay the factor expenses in other countries.
Sources of Foreign Currency
- Payment from Export of Goods and Services: When goods or services are exported to some other countries, it leads to increase in the reserve of the forex.
- Investment: When some people of other countries want to invest in our country for that foreign currency is needed and it leads to increase in the volume of foreign reserve.
- Loan from other Countries: Loan from other countries leads to increase in the foreign reserve of the country.
- Income Receipts: When some factor income is received from other countries.
- Donations: Donations from other world leads to increase the foreign currency in a country.
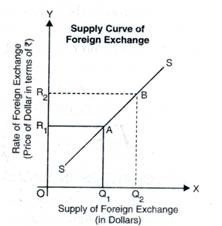
Demand and Supply Curve of Foreign Exchange Rate
The Demand Curve of the foreign exchange slopes downward due to the negative relationship between the demand of foreign exchange and rate of foreign exchange.
In the above curve, Q$ shows the demand of the foreign exchange.
The Supply Curve of the foreign exchange slopes upward due to the positive relationship between the supply of foreign exchange and rate of foreign exchange.
In the above curve, S shows the supply of the foreign exchange.
Reasons for Rise in Demand and Supply of Foreign Currency
The demand of foreign currency rises due to the following factors:
- When foreign currency is cheaper than the domestic currency.
- When the foreign product is cheaper than the domestic product due to which imports rises because of which people tends to buy more from foreign and for that payment is to be made in the foreign currency.
- When prices of foreign currency falls due to which the demand of foreign currency rises
The supply of foreign currency rises due to the following factors:
- When the foreign currency becomes more expensive than the domestic currency.
- When the domestic product becomes cheaper than the foreign product.
- When prices of foreign currency rises due to which supply of the same also rises.
Determination of Foreign Exchange Rate
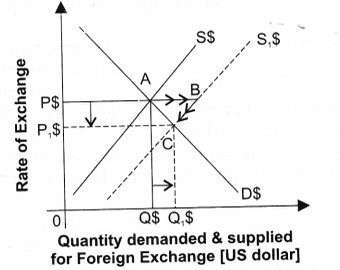
When the demand for foreign currency is equal to the supply of the foreign currency in that case the point where both of them cut each other is the point of equilibrium foreign exchange.
In the above diagram, the point E is the equilibrium point as that is the point where the demand of foreign currency (D) cuts the supply of foreign exchange (S) and P is the rate/ price of the foreign currency.
Condition Makes Foreign Exchange Rate Disequilibrium
There are two main reasons which makes equilibrium exchange rate disequilibrium which are as follows:
- Change in Demand: The change or disequilibrium occurs when the demand of foreign currency changes which can be further classified into two categories:
Increase in Demand: When the demand for foreign currency rises, it leads to shift in the demand curve to the upward and makes the equilibrium rate disequilibrium which leads to payment of more Indian rupees to get the same unit of the foreign currency i.e. Indian currency depreciate or foreign currency appreciates.
Decrease in Demand: When the demand for foreign currency falls, it leads to shift in the demand curve the downward and makes the equilibrium rate disequilibrium which leads to payment of less of Indian rupee to get the same unit of the foreign currency i.e. Indian currency appreciates or foreign currency depreciates.
- Change in Supply: The change or disequilibrium occurs when the supply of foreign currency changes which can be further classified into two categories:
Increases in Supply: When the supply for foreign currency increases, it leads to shift in the supply curve to the rightward and makes the equilibrium rate disequilibrium which leads to payment of fewer Indian rupees to get the same unit of the foreign currency i.e. Indian currency appreciates or foreign currency depreciates.
Decreases in Supply: When the supply for foreign currency decreases, it leads to shift in the supply curve to the leftward and makes the equilibrium rate disequilibrium which leads to payment of more Indian rupees to get the same unit of the foreign currency i.e. Indian currency depreciates or foreign currency appreciates.
Types of Exchange Rate – Merits and Demerits
- Fixed Exchange Rate: A rate is said to be fixed when it is fixed by the government to maintain the stability in the international market. When foreign rate rises, RBI on the behalf of the government sells foreign currency in the international market due to which the supply increases in the international market and the foreign exchange rate decreases whereas in the case of decrease in foreign rate, RBI buys foreign currency to increase the demand in the international market. This process is known as pegging or adjustable peg system.
Under this system, when the demand for domestic currency decreases in the international market, it is known as Devaluation of domestic currency whereas when the demand for domestic currency increases in the international market, it is known as Revaluation of domestic currency.
Merits:
Stability: Under this method of exchange rate, there is a stability of the exchange rate in the international money market
Long-term agreements: under this rate, long term bilateral trade agreements can be made in the international market because of stability in the policies of the government.
Demerits:
Huge Reserves: Under this rate, huge reserves of gold are made as different currencies have a direct or indirect impact on the gold.
International Growth: The international growth suffers as it does not allow the movement of capital across borders.
- Flexible Exchange Rate: A rate is said to be flexible when it is determined by the free play of the market. Under this system, RBI does not intervene in the increase or decrease in the rate of foreign exchange and leave all the work on the foreign exchange market to adjust the price.
Under this system, when the demand for domestic currency decreases in the international market, it is known as Depreciation of domestic currency whereas when the demand for domestic currency increases in the international market, it is known as Appreciation of domestic currency.
Merits:
International Reserves: Under this system, there is no need for the reserves as the rates are directly related to the own value of the currency.
International Growth: The international growth also does not suffer for it allows the movement of capital across borders.
Demerits:
Instability: Under this, the rates tends to fluctuate more and cause instability in the international market.
Long-term Agreements: Under this, it is difficult to make bilateral trade agreements as the rate of foreign currency changes like the price of goods in the international market.
Foreign Exchange Market
Foreign exchange market refers to the market under which the currencies of different countries are traded or sale and purchase transactions take place.
Functions of Foreign Exchange Market
- Hedging function: This function protects against the risk of fluctuation in the foreign rates by locking the price for agreements.
- Transfer Function: This function allows to transfer the power of purchase to different countries.
- Credit Function: This function allows the formation of credit in terms of foreign currency for the purpose of import and export.
Operations in Foreign Exchange Market
- Spot Market: It is also known as current market and operates in the daily nature of transactions. The rate that prevails in this market is known as spot rate or the rate at which the foreign currency is available at the spot.
- Forward Market: It refers to the market in which the delivery is made in the future date. The rate that prevails in this market is known as forward rate or the rate at which the foreign currency can be bought or sold on some future date.
Other Important Terms
- Parity Value: It is also known as mint parity or mint par value. Under this, the value of one currency is defined in terms of the value of other goods i.e. gold.
- Wider Band System: It is that system of fixed exchange rate which allows wider adjustment in the rate i.e. more than 10%.
- Crawling Peg System: It is that system of fixed exchange rate which allows smaller adjustment in the rate i.e. not more than 1% and it is known as crawl because it occurs on regular intervals.
Kindly refer to the following chapters for better understanding and higher scores in Class 12 Economics Exam.
|
|
Do share this post if you liked the notes of Foreign Exchange Rate Class 12. For more updates, subscribe to our website BrainyLads