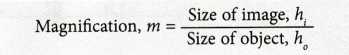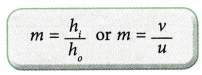December 24, 2021

Ray Optics and Optical Instruments Notes Class 12 | Term 2 | Physics

By admin Class 12 Physics Term 2 0 Comments

Table of Contents

Ray Optics and Optical Instruments Notes | Class 12 Physics | Term 2

Optics – It is the branch of physics that deals with the study of nature , production and propagation of light . It has two sub-branches : ray optics and wave optics .

Ray and geometrical optics- Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of rays. The ray in geometric optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances.

Wave or physical optics – Wave optics also called Physical optics deals with the study of various phenomena such as polarization, diffraction, interference and other occurrences where ray approximation of geometric optics cannot be done.

Laws of Reflection of Light

- The angle of reflection is equal to the angle of incidence (angle between incident ray and the normal). <i = <r
- The incident ray, reflected ray and the normal to the reflecting surface at the point of incidence all lie in the same plane.

Note: – These laws are valid at each point on any reflecting surface whether plane or curved.

The incident ray, reflected ray and the normal to the reflecting surface lie in the same plane.

Properties of Images Formed by Plane Mirror

Virtual and erect.
Behind the mirror.
The size of the image is equal to the size of the object.
Laterally inverted image (image of the left side visible on the right side).
The distance of the image behind the mirror is the same as the distance of an object from the mirror.

Spherical Mirror

A spherical mirror is a part of a reflective spherical surface and they are in sphere in shape.
It is made up of a large number of extremely small plane mirrors.

Spherical Mirrors are of two types-

Concave Mirror: –

They are silvered on the inside of sphere.
It is a converging mirror.
In a Concave mirror when the rays of light reflect back they meet or converge at a point that is why known as converging mirror.

Convex Mirror: –

They are silvered on the outside of sphere.
In Convex mirror the rays don’t meet at appoint after reflection that is why it is a diverging mirror.

Some terminologies related to Spherical Mirrors-

Pole:

The centre of the reflecting surface of a spherical mirror.
It lies on the surface of the mirror.
The pole is usually represented by the letter P.

Centre of Curvature:

The reflecting surface of a spherical mirror forms a part of a sphere. The sphere’s centre is called as centre of curvature.
It is represented by the letter C.
The centre of curvature is not a part of the mirror. It lies outside its reflecting surface.
The centre of curvature of a concave mirror lies in front of it.
However, it lies behind the mirror in case of a convex mirror.

Radius of Curvature

The radius of the sphere of which the reflecting surface of a spherical mirror forms a part
It is represented by the letter R.

Principal Axis

A straight line passing through the pole and the centre of curvature of a spherical mirror.
Principal axis is normal to the mirror at its pole.

Principal Focus

Rays parallel to the principal axis falling on a concave mirror meet/intersect at the point on the principal axis. The point is called principal focus of concave mirror.
The reflected rays appear to come from a point on the principal axis when rays parallel to the principal axis fall on a convex mirror, that point is called principal focus of convex mirror.
The principal focus is represented by the letter F.
The distance between the pole and the principal focus of a spherical mirror is called the focal length. It is represented by the letter f.

Aperture

The diameter of the reflecting surface of spherical mirror is called its aperture.
Mirrors whose aperture is much smaller than its radius of curvature, we use R=2f.

Sign Convention for Spherical Mirrors (Concave and Convex Mirrors)

Distances are to be measured from the pole (vertex) of the mirror marked by point V in the figure.
Distances measured along the direction of the incident ray are positive. The distance measured opposite the direction of the incident ray are negative.
Distances measured above the principal axis are positive. Distances measured below the principal axis are negative.

Linear or Transverse magnification

Linear (sometimes called lateral or transverse) magnification refers to the ratio of image length to object length measured in planes that are perpendicular to the optical axis. A negative value of linear magnification denotes an inverted image.

Linear magnification = length of image / length of object = v/u

Mirror Formula

Concave Mirror
(1/v) + (1/u) = (1/f)
Where:-
The distance of the object from its pole is called the object distance (u).
The distance of the image from the pole of the mirror is called the image distance (v).
The distance of the principal focus from the pole is called the focal length (f).
Mirror equation relates image distance (v) with object distance (u) and focal (f) length
Consider a concave mirror, an object AB placed in the front of the concave mirror. The image produced is A’B’.
Consider two right-angled similar triangles A’B’F and MPF.
Therefore (B’A’/PM) = (B’F/FP)
Or (B’A’/BA) = (B’F/FP) (because PM= AB) (1)
Since <APB = <AP’B’, the right angles triangles are also similar.
Therefore, (B’A’/BA) = (B’P’/BP) (2)
Comparing equations (1) and (2):-
(B’F/FP) = (B’P –FP)/(FP) = (PB’)/(PB) equation (A)
Considering the sign conventions:
- Light travels from the object to the mirror MPN. Hence this is taken as the positive direction.
- The object AB, image A′B′ as well as the focus F from the pole P, we have to travel opposite to the direction of incident light.
- Therefore all are taken as negative.
- This implies, B’P = -v , FP =-f and BP =-u
- Therefore equation(A) changes to:
  - (-v –f)/(-f) = (-v/-u)
  - Or (v-f)/(f) =(v/u)
  - => (1/v) +(1/u) = (1/f)
- This relation is known as the mirror equation.

(Concave mirror)

(b) In case of convex mirror

Using equation (A) (B’F/FP) = (B’P –FP)/(FP) = (PB’)/(PB)
Image Distance PB’ = (+v) as it is measured from the pole and in the direction of the incident ray.
PF= + f as it is also along the incident ray.
Object distance PB= (-u) as it is in the direction opposite to the incident ray.
Substituting the values,
- (v-f)/(u) = (+v/-u)
- =>(v/f) – 1 = ((-v/u)
- Dividing throughout by f,
- (1/f) – (1/v) =(-1/u)
- Or (1/f) = (1/v) –(1/u)
Therefore the mirror equation will be:- (1/f) = (1/v) –(1/u)

Magnification of a Spherical Mirror

Linear Magnification (m) produced by a spherical mirror gives the relative extent to which the image of an object is magnified with respect to the object size.
Mathematically,
m= (height of the image h’)/(height of the object h)
Or, m = (h’)/(h)
If the sign of magnification is negative then the image is real and if it is positive then the image is virtual.
A real, inverted image is formed by a concave mirror.
In triangles A′B′P and ABP, we have,
(-B’A’/BA) =(-B’P)/(BP) (From equation 2)
Applying sign convention, this becomes
(– h’/h) = -(-v/- u)
Therefore, m = (h’/h) = (- v/u)

Concave Mirror

In case of convex mirror: Virtual and erect image is formed.
m = (h’/h) = (A’B’)/(AB) = (PB’)/(PB)
m= -(v/u)

Convex Mirror

Note: – It is valid for all the cases of reflection by a spherical mirror (concave or convex) whether the image formed is real or virtual

Refraction of light-

It is the phenomenon of bending of light from its straight path when it passes an angle from one transparent medium to another.

Laws of refraction given by Snell’s law:

The incident ray, the refracted ray and the normal to the interface at the point of incidence, all lie in the same plane.
The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant.
- The angles of incidence (i) and refraction (r) are the angles that the incident and its refracted ray make with the normal, respectively.
  - n₂₁ = (sin i)/(sin r)
  - Where n₂₁ = is a constant known as refractive index of the second medium with the first.
  - $Class_12_Physics_Ray_Optics_Laws_Of_Refraction$
    - Note: – The refractive index (n₂₁) depends on the wavelength of light, also characteristic of pair of media.
    - It is independent of the angle of incidence. $Class_12_Physics_Ray_Optics_Laws_Of_Refraction1$

- - - If n₂₁ >1, r<i then the refracted ray bends towards the normal. Medium 2 will be optically denser. So medium 2 is called optically denser medium as compared to medium 1.
    - If n₂₁ <1, r>i then the refracted ray bends away from the normal. Medium 2 will be optically denser. So medium 2 is called optically rarer medium as compared to medium 1.

Refraction through a parallel-side slab

For a rectangular slab, refraction takes place at two interfaces (air-glass and glass-air).
From the diagram it is clear that r₂=i₁e. emergent ray is parallel to the incident ray, there will be no deviation.
But there will be lateral shift w.r.t the incident ray.
Refractive index of medium 3 w.r.t medium 1 n₃₁ =(n₃/n₁)
Or n₃₁ = (n₃/n₂) x (n₂/n₁) = (n₃₂ x n₂₁)
- Where
- n₁ = refractive index of medium 1
- n₂ = refractive index of medium 2
- n₃ = refractive index of medium 3
It can be written as: – (n₃₁ x n₂₁) where n₃₁ is the refractive index of medium 3 w.r.t medium 1.

$Class_12_Physics_Ray_Optics_Refraction_By_Glass_Slab$

Refraction & Natural Phenomena

The refraction of light through the atmosphere is responsible for many interesting phenomena.

Advanced Sunrise and Delayed Sunset:-

For example, the sun is visible a little before the actual sunrise and until a little after the actual sunset due to refraction of light through the atmosphere.
By actual sunrise we mean the actual crossing of the horizon by the sun.
The figure shows the actual and apparent positions of the sun with respect to the horizon. The refractive index of air with respect to vacuum is 1.00029.
Due to this, the apparent shift in the direction of the sun is by about half a degree and the corresponding time difference between actual sunset and apparent sunset is about 2 minutes.
The apparent flattening (oval shape) of the sun at sunset and sunrise is also due to the same phenomenon.

Twinkling of Stars:-

All the stars have light of their own. Stars twinkle because by the time the light reaches our eye, it passes through the various layers of the atmosphere.
At one point of time star appears to be at one position and at another minute it appears to be at another position.
So if we see one object at two different places at a very frequent interval of time. Therefore we feel that the star is twinkling.
This twinkling of star is also the phenomenon of refraction of light.

Principle of Reversibility of Light

The principle of reversibility of light states that light follows the same path if the direction of the travel of light is reversed.

The principle of reversibility presumes that the attenuation of a light ray during its passage through an optical medium because of reflection, refraction, and absorption is not affected by a reversal of the direction of the ray. In its simplest explanation, the principle of reversibility is a deduction of Snell’s law of the refraction of light. The principle of reversibility presumes that the attenuation of a light ray during its entrance through an optical medium due to reflection, refraction, and absorption is not changed by a reversal of the direction of the ray.

Principle of Reversibility of light

If the direction of a ray of light is reversed due to reflection off a surface, then it will retrace its path.

Total Internal Reflection

When light travels from an optically denser medium to a rarer medium at the interface, it is partly reflected back into the same medium and partly refracted to the second medium. This reflection is called the internal reflection.
In total internal reflection phenomenon there is no refraction and the entire incident ray will get reflected.
Conditions for Total Internal Reflection are as follows:-
- Light ray travels from denser to rarer medium.
  - When a ray of light moves from a denser medium to a rarer medium it moves away from the normal. The ray will get refracted at an r (angle of refraction).
  - But if we keep increasing angle of incidence it will further move from normal and the angle of refraction will become less.
  - A condition will come if we keep on increasing the angle of incidence, the angle of refraction will become equal to 90⁰ and further increase in angle of incidence there will be no refraction will occur but reflection will take place.
  - This is total internal reflection.
  - The limiting factor beyond what total internal reflection will take place will be :-
    - The angle of incidence should be greater than the angle of incidence for which angle of refraction is 90⁰.
  - Angle of incidence should correspond to angle of refraction = 90⁰.
  - This angle is known as Critical angle.
  - Angle of incidence should be greater than Critical angle.
- Total internal Reflection is an optical phenomenon observed when a ray of light travelling from denser to rarer medium strikes the boundary at an angle greater than the critical angle.

Applications of Total Internal Reflection

Optical Fibres:-
- They are used in telecommunication industries.
- Optical fibres work on the phenomenon of total internal reflection.
- Characteristics of Optical Fibres:-
  - They are small in size and light in weight.
  - They have greater information carrying capacities than metallic wires.

Working of Optical fibres:

Optical fibres are fabricated with high quality composite glass/quartz fibres.
Each fibre consists of a core and cladding. The refractive index of the material of the core is higher than that of the cladding.
As there is difference in the refractive index of core and denser; core acts as a denser medium and cladding acts as a rarer medium.

When a signal in the form of light is directed at one end of the fibre at a suitable angle, it undergoes repeated total internal reflections along the length of the fibre and finally comes out at the other end.
Since light undergoes total internal reflection at each stage, there is no appreciable loss in the intensity of the light signal.
Optical fibres are fabricated such that light reflected at one side of inner surface strikes the other at an angle larger than the critical angle.
Even if the fibre is bent, light can easily travel along its length. Thus, an optical fibre can be used to act as an optical pipe.
They are made up of plastic.

Glass vs. Plastic Optical Fibres

Plastic Optical fibres	Glass Optical fibres
1.Cheaper	They are not so cheap.
2. Flexible	They are not so flexible.
3. They can withstand more stress.	They cannot withstand more stress.
4. Less efficient transmission.	More efficient transmission over large distances.

Applications of Optical Fibres

Fibre Optic endoscopy

Decorative items

They are used in communication system

Prism

Prisms make use of total internal reflection which makes it useful in binoculars.
Prisms designed to bend light by 90º or by 180º make use of total internal reflection.
Such a prism is also used to invert images without changing their size.
In the first two cases, the critical angle i_c for the material of the prism must be less than 45º.

Lens

A lens is a piece of a refracting medium bounded by two surfaces , at least one which is a curved surface .

Lenses are of two types:

Convex lens

The convex lens is a lens that converges rays of light that convey parallel to its principal axis (i.e. converges the incident rays towards the principal axis) which is relatively thick across the middle and thin at the lower and upper edges.

Concave lens

A concave lens is a lens that possesses at least one surface that curves inwards. It is a diverging lens, meaning that it spreads out light rays that have been refracted through it

Optical centra: The centre point of a lens is known as its optical centre. It always
lies inside the lens. A light beam passing through the optical centre immerges without any deviation.
Centra of curvature: It is defined as the centre of the spheres of which the lens is originally a part of. Because the spherical lens consists of two spherical surfaces, the lens has two centres of curvature.
Principal axis: The line joining the centre of curvature and the optical centre is called the principal axis.
Aperture: This is the length or breadth of the lens through which refraction takes place.
Principal focus: A light ray parallel to the principal axis of the lens meets at a point on the principal axis. This point is called the principal focus.
Focal length: The distance of the point from the centre of lens or mirror at which a parallel ray of beam converge (or diverge) is called focal length and the point is called focus.

New Cartesian Sign Convention for spherical lenses:

(i) All the distances are measured from the optical centre of the lens.

(ii) The distances measured in the same direction as that of incident light are taken as positive.

(iii) The distances measured against the direction of incident light are taken as negative.

(iv) The distances measured upward and perpendicular to the principal axis are taken as positive.

(v) The distances measured downward and perpendicular to the principal axis are taken as negative.

Refraction through a spherical mirror

Refraction at a spherical interface between two transparent media. An infinitesimal part of a spherical surface can be regarded as planar and the same laws of refraction can be applied at every point on the surface.

$Class_12_Physics_Ray_Optics_Refraction_By_Spherical_Surfaces$

The rays are incident from a medium of refractive index n₁, to another of refractive index n₂.
Assuming the aperture (or the lateral size) of the surface to be small compared to other distances involved, so that small angle approximation can be made.
Consider NM will be taken to be nearly equal to the length of the perpendicular from the point N on the principal axis.
Considering small angles,
- tan<NOM = (MN)/(OM)
- tan < NCM = (MN/MC)
- tan<NIM = (MN)/(MI)
- Now, for ΔNOC, <i is the exterior angle. Therefore, i = ∠NOM + ∠NCM
- i = (MN/OM)+(MN/MC) (equation (1))
- Similarly, r = ∠NCM – ∠NIM
- e., r = (MN/MC) – (MN/MI) (equation (2))
- Now, by Snell’s law n₁ sin i = n₂ sin r or for small angles
- n₁i = n₂r
Substituting i and r from Equation. (1) and (2), we get
(n₁/OM) + (n₂/MI) = (n₂ – n₁)/MC) Equation (3)
Here, OM, MI and MC represent magnitudes of distances. Applying the Cartesian sign convention,
OM = –u, MI = +v, MC = +R
Substituting these in Eq. (3), we get,
(n₂ –v) –(n₁/u) = (n₂ – n₁)/(R) Equation (4)
Equation (4) gives us a relation between object and image distance in terms of refractive index of the medium and the radius of curvature of the curved spherical surface.

Lens maker’s formula

This formula relates the focal length f of the refractive index μ and the radii of curvature R1 , R2 of its spherical surfaces .

Linear Magnification produced by a lens

It is the ratio of the size of the image formed by a lens to the size of the object.

- The simplest way to compare the image with the object is by the ratio of their sizes. This ratio is the linear magnification.

The ratio of the image size to the object size is the same as the ratio of the image distance to the object distance.
In symbols,

Lens combinations

When lenses are used in combination , each lens magnifies the image formed by the preceding lens. The total magnification is equal to the product of the magnifications produced by the individual lenses.

Combined focal length (F): =f 1 f 2 /[f 1 + f 2] F

Refraction through prism

A prism is a portion of a refracting medium bounded by two plane faces inclined to each other at a certain angle. the two plane faces inclined to each other are called refracting surfaces . The line along which the two refracting faces meet is called refracting faces . The line along which the two refracting faces meet is called refracting edge of the prism. The third face of the prism is opposite to the refracting edge is called base of the prism .

Prism is a transparent optical material with flat polished surfaces that refract light.

Terminologies

Incident Ray: – The ray which enters the prism.
Refracted Ray: – The ray which comes out of prism inside the prism.
Emergent Ray: – The ray which comes out of prism.
Angle of deviation δ:-The angle which will tell how much the emergent ray deviated from the original incident ray.
Angle of Prism: – The angle of the prism <A is known as angle of prism.

$Class_12_Physics_Ray_Optics_Refraction_By_Prism$

The angles of incidence and refraction at the first face AB are i and r₁, while the angle of incidence (from glass to air) at the second face AC is r₂ and the angle of refraction or emergence (e).
The angle between the emergent ray RS and the direction of the incident ray PQ is called the angle of deviation, δ.
Consider the quadrilateral AQNR, in the figure two angles (at the vertices Q and R) are right angles.
<A + <QNR = 180⁰ (As sum of other angles of a quadrilateral is 180⁰).
From the triangle QNR,(r₁ + r₂ + ∠QNR) = 180º
Comparing these two equations, we get

(r₁ + r₂ = A) (Equation 1)

The total deviation δ is the sum of deviations at the two faces,
δ = (i – r₁ ) + (e – r₂ ) that is,
δ = (i + e – A) (Equation 2)
Thus, the angle of deviation depends on the angle of incidence.
Relation between angle of deviation and angle of incidence:-

As the angle of incidence increases the angle of deviation keep on decreasing and when it reaches a point where angle of incidence is equal to angle of emergence, then the angle of deviation is minimum, and again it will start decreasing.
This implies angle of deviation is minimum

δ_min when angle of incidence <i = angle of emergence <e.

Angle of Deviation

At the minimum deviation D_min, the refracted ray inside the prism becomes parallel to its base.
Therefore, we have δ = D_m, i = e which implies r₁ = r₂.
From (Equation 1) 2r = A or r = (2/A)
In the same way, (Equation 2) gives

D_m = (2i – A), or i = ((A + D_m)/2) (Equation 3)

The refractive index of the prism is

n₂₁ = (n₁/n₂)

=sin [(A + D_m)/2]/ (sin [A/2])

≈ ((A + Dm)/ (2))/ (A/2)

The angles A and D_m can be measured experimentally. Equation (3) thus provides a method of determining refractive index of the material of the prism.
For a small angle prism, i.e., a thin prism,

D_m, is also very small = (n₂₁ -1) A

It implies that, thin prisms do not deviate light much.

Dispersion

The splitting of white light into its constituent colours when it passes through a glass prism is called dispersion. the dispersion of light occurs because refractive index of prism material is different for different wavelengths.

Angular dispersion

The angular separation between the two extreme colours ( violet and red) in the spectrum is called angular dispersion .

Angular dispersion

θ=δv−δr=(μv−μr)A.

Dispersion power

It is the ability of the prism material to cause dispersion and is defined as the ratio of the angular dispersion the mean deviation .

Dispersion power: Dispersive power of a prism is defined as the ratio of angular dispersion to mean deviation produced by prism. ω=δδv−δr=μ−1μv−μr.

Spherical aberration

The inability of a lens or spherical mirror of large aperture to bring the paraxial and marginal rays of a wide beam of light to focus at a single point is called spherical aberration.

Chromatic aberration

The inability of a lens or spherical mirror of large aperture to bring the light rays of different colours to focus at a single point is called chromatic aberration.

Rayleigh’s law of scattering-According to this law, first derived in 1871 by Lord Rayleigh using simple dimensional arguments, scattering in all directions by an object is inversely proportional to the fourth power of the wavelength of the illumination.

Rainbow-It is nature’s most spectacular display of the spectrum of light produced by refraction , dispersion and total internal reflection of sunlight by several raindrops. It is observed when the sun shines on rain drops after a shower . An observer it in the form of concentric circular arcs of different colours in the horizon.

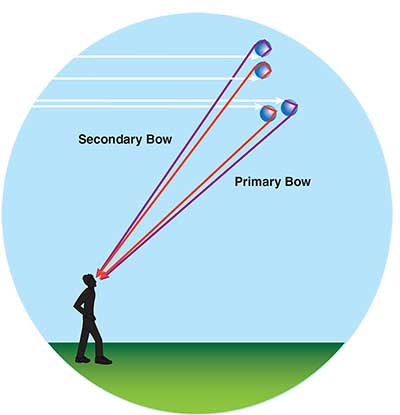
Primary rainbow-One total internal reflection and two refractions of white light by water droplets produce the primary rainbow.

The primary rainbow is caused from one reflection inside the water droplet. The secondary rainbow is caused by a second reflection inside the droplet, and this “re-reflected” light exits the drop at a different angle (50° instead of 42° for the red primary bow). This is why the secondary rainbow appears above the primary rainbow. The secondary rainbow will have the order of the colors reversed, too, with red on the bottom and violet on the top.

Human Eye – It is the most important and sensitive sense organ . The essential parts of a human eye are sclerotic , cornea, choroid , iris , pupil , crystalline lens , ciliary muscles , aqueous humour , viterous humour and retina . It is a convex lens of focal length about 2.5 cm .

Accommodation

It is the ability of the eyelens due to which it can change its focal length so that images of objects at various distances can be formed on the same retina.

Range of normal vison

The distance between infinity and 25cm point is called the range of normal vision .

Least distance of distinct vision

it is the distance from the eyes up to which eyes can have a clear vision is called least distinct vision. It is about 25cms for a normal healthy eye. Thus adult eyes can see the object from infinity to 25cm.

Power of accommodation

The power of accommodation of the eye is the maximum variation of its power for focussing on near and far objects . For a normal eye , the power of accommodation is about 4 dioptres.

Persistence of vision

The persistence of vision of normal human eye is 1/16 s. … The human eye and brain can only process about 12 separate images per second, retaining an image for 1/16 of a second.

Common defects of vision

a. Myopia or Near-Sightedness

Myopia is a defect of vision wherein far-off objects appear blurred and objects near are seen clearly. Since the eyeball is too long or the eye lens’s refractive power is too high; the image forms in front of the retina rather than forming on it. Correction of myopia can happen by wearing glasses/contacts made of concave lenses to help focus the image on the retina.

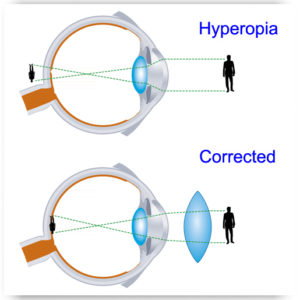
b. Hypermetropia or Longsightedness

Hypermetropia is a defect of vision wherein there is difficulty in viewing objects that are near but one can view far objects easily. Since the eyeball is too short or eye lens’s refractive power is too weak hence the image instead is of being forming upon the retina, its forms behind the retina. Correction of hypermetropia can happen by wearing glasses/contacts containing convex lenses.

Source: Optometriceyesitenc.com

c. Cataract

Cataract is the clouding of the lens, that prevents the formation of a clear, sharp image. A cataract forms when old cells after they die, stick in a capsule wherein with time a clouding over lens happens. Because of this clouding blurred images are formed. Correction of cataract can happen through a surgery. An artificial lens in place of the opaque lens is after removing it via surgery.

d. Presbyopia or Old-age Longsightedness

Presbyopia is a natural defect that occurs with the age. In presbyopia, the ciliary muscles become weak and are no longer able to adjust the eye lens. The eye muscles become so weak that no longer can a person see nearby objects clearly. The near point of a person with presbyopia is more than 25cm. Correction of presbyopia can happen by wearing bifocal glasses or Progressive Addition Lenses (PALs) wherein the upper portion of the lens contains concave lens and lower portion contains a convex lens.
A person with presbyopia can also have just myopia or just hypermetropia.

e. Astigmatism

Astigmatism is a defect wherein the light rays entering the eye do not focus light evenly to a single focal point on the retina but instead scatter away. The light rays in a way where some focus on the retina and some focus in front of or behind it. This happens because of non-uniform curvature of the cornea; resulting in a distorted or blurry vision at any distance. Correction of astigmatism can happen by using a special spherical cylindrical lens.

Simple microscope

A simple microscope is a magnifying glass that has a double convex lens with a short focal length. The examples of this kind of instrument include the hand lens and reading lens. When an object is kept near the lens, then its principal focus with an image is produced, which is erect and bigger than the original object. The formed image is virtual and cannot be projected on a screen like a real image.

Magnification Of Simple Microscope

The magnifying power formula of a simple microscope is given as:

M = 1 + \frac{D}{F}

Where,

D is the least distance of the distinct vision
F is the focal length of the convex lens

Compound Microscope

In order to have large magnifications compound microscope is used.

The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual.
The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point.
Clearly, the final image is inverted with respect to the original object.
Using tanβ = (h/f₀) = (h’/L)
Magnification (m_o) due to objective = (h’/h) =(L/f₀)
- Where h’ = size of the first image
- h= size of the object
- f_o = focal length of the objective lens
- f_e= focal length of the eye-piece
- L (tube length) = Distance between focal length of the second objective lens and the first focal length of the eye-piece.
When the final image is formed at the near point, then the angular magnification will be :-
m_e=(1+(D/f_e))
When the final image is formed at infinity, the angular magnification due to the eyepiece is:-
m_e = (D/f_e)
Total magnification will be given as:-
m=(m_om_e) =(L/f₀)(D/f_e)
Note: – In order to achieve a large magnification of a small object (hence the name microscope), the objective and eyepiece should have small focal lengths. In practice, it is difficult to make the focal length much smaller than 1 cm.

Telescope

An instrument used to view distant objects clearly.
It consists of:- (a) Objective lens (b) Eyepiece

Working of Telescope

The telescope is used to provide angular magnification of distant objects. The objective has a large focal length and a much larger aperture than the eyepiece because object is very far away.
Light from a distant object enters the objective and a real and inverted image is formed at its second focal point.
This image acts as an object for the eyepiece; it magnifies this image producing a final inverted image.

Magnification

The magnifying power m is the ratio of the angle β subtended at the eye by the final image to the angle α which the object subtends at the lens or the eye.
Therefore, m≈ (β / α) ≈ (h/f_e) x (f_o/h) = (f_o/h).
In this case, the length of the telescope tube is (f_o + f_e).
In addition, a pair of inverting lenses to make the final image erect.
Refracting telescopes can be used both for terrestrial and astronomical observations.

Related

Electromagnetic Waves	Semiconductors
Atoms	Dual Nature of Radiation and Matter
Wave Optics	Ray Optics and Optical Instrument
Nuclei	NCERT Solutions of Class 12 English
NCERT Solutions of Class 12 Physics	NCERT Solutions of Class 12 Chemistry
NCERT Solutions of Class 12 Biology	Writing Section Class 12 English

Do share this post if you liked Ray Optics and Optical Instruments Notes Class 12. For more updates, keep logging on BrainyLads.

Properties of Images Formed by Plane Mirror

Spherical Mirror

Principle of Reversibility of Light

Related Posts

Add a Comment